题目内容
已知θ∈(0,2π),满足不等式cosθ<sinθ和tanθ<sinθ的θ的取值范围是
- A.
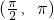
- B.

- C.

- D.

A
分析:根据三角不等式和三角函数的性质,求出不等式的解集,再由θ∈(0,2π)求出θ的取值范围.
解答:∵cosθ<sinθ且tanθ<sinθ,
∴ 且
且 或
或 ,
,
∴所求的解集是 ,
,
又∵θ∈(0,2π),∴所求的θ的取值范围是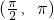 ,
,
故选A.
点评:本题的考点是利用三角函数性质求三角函数的不等式,需要根据题意列出三角函数的不等式,再由三角函数的性质求出解集,结合已知的范围再求出交集.
分析:根据三角不等式和三角函数的性质,求出不等式的解集,再由θ∈(0,2π)求出θ的取值范围.
解答:∵cosθ<sinθ且tanθ<sinθ,
∴
 且
且 或
或 ,
,∴所求的解集是
 ,
,又∵θ∈(0,2π),∴所求的θ的取值范围是
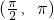 ,
,故选A.
点评:本题的考点是利用三角函数性质求三角函数的不等式,需要根据题意列出三角函数的不等式,再由三角函数的性质求出解集,结合已知的范围再求出交集.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目