题目内容
某市直小学为了加强管理,对全校教职工实行新的临时事假制度:“每位教职工每月在正常的工作时间,临时有事,可请假至多三次,每次至多一小时”.现对该制度实施以来50名教职工请假的次数进行调查统计,结果如下表所示:
| 请假次数 |  | 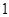 | 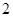 | 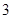 |
| 人数 | 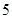 | 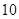 | 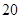 | 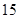 |
(1)从该小学任选两名教职工,用
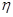 表示这两人请假次数之和,记“函数
表示这两人请假次数之和,记“函数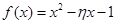 在区间
在区间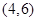 上有且只有一个零点”为事件
上有且只有一个零点”为事件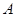 ,求事件
,求事件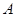 发生的概率
发生的概率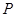 ;
;(2)从该小学任选两名职工,用
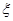 表示这两人请假次数之差的绝对值,求随机变量
表示这两人请假次数之差的绝对值,求随机变量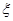 的分布列及数学期望
的分布列及数学期望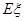 .
.
(1)
(2)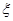 的分布列:
的分布列: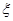
0 1 2 3 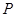




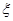 的数学期望:
的数学期望: .
.
解析试题分析:(1) 函数 过
过 点,在区间
点,在区间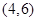 上有且只有一个零点,则必有
上有且只有一个零点,则必有 即:
即: ,解得:
,解得: ,所以,
,所以, 或
或 ……3分
……3分
当 时,
时, ,当
,当 时,
时, …………5分
…………5分 与
与 为互斥事件,由互斥事件 的概率公式,所以
为互斥事件,由互斥事件 的概率公式,所以 6分
6分
(2) 从该小学任选两名教职工,用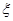 表示这两人请假次数之差的绝对值,则
表示这两人请假次数之差的绝对值,则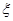 的可能取值分别是
的可能取值分别是 ,于是
,于是
 ,
, ,
, 10分
10分
从而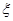 的分布列:
的分布列: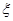
0 1 2 3 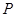




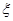 的数学期望:
的数学期望: . …………12分
. …………12分
考点:古典概型
点评:主要是考查了分布列和古典概型概率的计算,属于基础题。

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
为了考察某种中药预防流感效果,抽样调查40人,得到如下数据:服用中药的有20人,其中患流感的有2人,而未服用中药的20人中,患流感的有8人。
(1)根据以上数据建立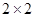 列联表;
列联表;
(2)能否在犯错误不超过0.05的前提下认为该药物有效?
参考
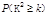 | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
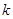 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
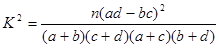 (
(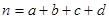 )
) 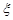 的分布列和数学期望.
的分布列和数学期望. 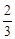 ,中奖可以获得2分;方案乙的中奖率为
,中奖可以获得2分;方案乙的中奖率为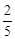 ,中奖可以获得3分;未中奖则不得分。每人有且只有一次抽奖机会,每次抽奖中奖与否互不影响,晚会结束后凭分数兑换奖品。
,中奖可以获得3分;未中奖则不得分。每人有且只有一次抽奖机会,每次抽奖中奖与否互不影响,晚会结束后凭分数兑换奖品。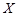 ,求
,求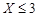 的概率;
的概率;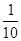 ,不堵车的概率为
,不堵车的概率为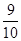 ;走公路Ⅱ堵车的概率为
;走公路Ⅱ堵车的概率为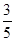 ,不堵车的概率为
,不堵车的概率为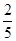 ,若甲、乙两辆汽车走公路Ⅰ,第三辆汽车丙由于其他原因走公路Ⅱ运送水果,且三辆汽车是否堵车相互之间没有影响.
,若甲、乙两辆汽车走公路Ⅰ,第三辆汽车丙由于其他原因走公路Ⅱ运送水果,且三辆汽车是否堵车相互之间没有影响.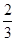 ,且各题答对与否互不影响.设选手甲、选手乙答对的题数分别为ξ,η.
,且各题答对与否互不影响.设选手甲、选手乙答对的题数分别为ξ,η. ,得到黑球或黄球的概率是
,得到黑球或黄球的概率是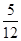 ,得到黄球或绿球的概率是
,得到黄球或绿球的概率是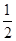 ,试求得到黑球、黄球、绿球的概率各是多少?
,试求得到黑球、黄球、绿球的概率各是多少?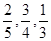 ,且假设各自能否被选中是无关的.
,且假设各自能否被选中是无关的.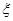 ,试求
,试求