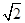题目内容
过定点 作直线
作直线 ,使
,使 与抛物线
与抛物线 有且仅有一个公共点,这样的直线
有且仅有一个公共点,这样的直线 共有( )
共有( )
| A.1条 | B.2条 | C.3条 | D.4条 |
C
解析试题分析:由题意直线l的斜率存在,故设为y=kx+2k+2,联立 消y得
消y得 ,当k=0时,方程化为x=1,此时只有一个公共点(1,2),当k≠0时,要使
,当k=0时,方程化为x=1,此时只有一个公共点(1,2),当k≠0时,要使 与抛物线
与抛物线 有且仅有一个公共点,则
有且仅有一个公共点,则 ,∴
,∴ ,∴
,∴ ,此时符合条件直线有两条,综上,满足题意的直线共有3条。
,此时符合条件直线有两条,综上,满足题意的直线共有3条。
考点:本题主要考查了直线与抛物线的位置关系。
点评:解决此类问题时要注意对直线斜率是否存在讨论。

练习册系列答案
相关题目
若点 在圆C:
在圆C:  的外部,则直线
的外部,则直线 与圆C的位置关系是( )
与圆C的位置关系是( )
| A.相切 | B.相离 | C.相交 | D.相交或相切 |
直线 与圆
与圆 相交于M、N两点,若
相交于M、N两点,若 ,则k的取值范围为( )
,则k的取值范围为( )
A. | B. | C. | D.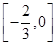 |
圆 和圆
和圆 的位置关系为( )
的位置关系为( )
| A.相交 | B.内切 | C.外切 | D.外离 |
已知直线 与圆
与圆 交于
交于 两点,且
两点,且 (其中
(其中 为坐标原点),则实数
为坐标原点),则实数 的值为
的值为
A. | B. | C. 或 或 | D. 或 或 |
两圆相交于点 ,两圆的圆心均在直线
,两圆的圆心均在直线 上,则
上,则 的值为( )
的值为( )
A. | B. | C. | D. |
若点P(1,1)为圆 的弦MN的中点,则弦MN所在直线的方程为( )
的弦MN的中点,则弦MN所在直线的方程为( )
A. | B. |
C. | D. |
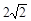 D、8
D、8 与圆
与圆 的两个交点,则
的两个交点,则 ( )
( ) D.
D.