题目内容
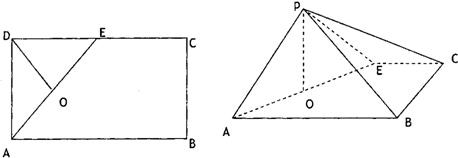
如图所示,在矩形ABCD中,AB=2BC=2a,E为AB上一点,将B点沿线段EC折起至点P,连接PA、PC、PD,取PD的中点F,若有AF∥平面PEC.
 (1)试确定E点位置;
(1)试确定E点位置;
(2)若异面直线PE、CD所成的角为60°,并且PA的长度大于a,
求证:平面PEC⊥平面AECD.
(1) E为AB的中点(2)证明略
解析:
(1) E为AB的中点.
证明如下:取PC的中点G,连接GE,GF.
 由条件知GF∥CD,EA∥CD,∴GF∥EA.
由条件知GF∥CD,EA∥CD,∴GF∥EA.
则G、E、A、F四点共面.
∵AF∥平面PEC,
平面GEAF∩平面PEC=GE,
∴FA∥GE.
则四边形GEAF为平行四边形.
∴GF=AE,∵GF=![]() CD,∴EA=
CD,∴EA=![]() CD=
CD=![]() BA.
BA.
即E为AB的中点.
(2) ∵EA∥CD,PE、CD所成的角为60°,且PA的长度大于a.
∴∠PEA=120°.
∵PE=BE=EA=a,∴PA=![]() a.
a.
取CE的中点M,连接PM,AM,BM,在△AEM中,
AM=![]() =
=![]() a.
a.
∵PM=BM=![]() a,∴PM2+AM2=PA2.
a,∴PM2+AM2=PA2.
则∠PMA=90°,PM⊥AM.
∵PM⊥EC,EC∩AM=M,
∴PM⊥平面AECD.
∵PM![]() 平面PEC,
平面PEC,
∴平面PEC⊥平面AECD.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
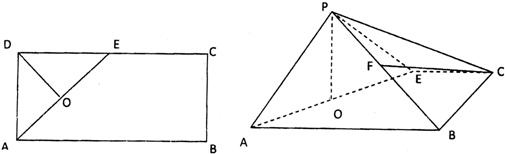 19、如图所示,在矩形ABCD中,AB=4,AD=2,E是CD的中点,O为AE的中点,以AE为折痕将△ADE向上折起,使D到P点位置,且PC=PB,F是BP的中点.
19、如图所示,在矩形ABCD中,AB=4,AD=2,E是CD的中点,O为AE的中点,以AE为折痕将△ADE向上折起,使D到P点位置,且PC=PB,F是BP的中点.
 如图所示,在矩形ABCD中,AB=4cm,BC=2cm,在图形上随机撒一粒黄豆,则黄豆落到圆上的概率是
如图所示,在矩形ABCD中,AB=4cm,BC=2cm,在图形上随机撒一粒黄豆,则黄豆落到圆上的概率是 如图所示,在矩形ABCD中,已知AB=a,BC=b.a≤3b,在AB,AD,CD,CB上分别截取AE,AH,CG,CF,且都等于x,则四边形EFGH面积的最大值为
如图所示,在矩形ABCD中,已知AB=a,BC=b.a≤3b,在AB,AD,CD,CB上分别截取AE,AH,CG,CF,且都等于x,则四边形EFGH面积的最大值为