题目内容
如图，| AE |
| AD |
| AB |
分析：利用向量加法的平行四边形法则可过E分别作AB，AD的平行线与AD，AB分别交于N，M点则可得
=
+
，即
+
=x
+y
，而由图形可得
与
，
与
共线故
=x，
=y即x+y=
+
，再结合EM∥AD，EN∥AB根据平行线分线段成比例性质代入化简即可得解．
| AE |
| AM |
| AN |
| AM |
| AN |
| AD |
| AB |
| AM |
| AB |
| AN |
| AD |
| AM |
| AB |
| AN |
| AD |
| AM |
| AB |
| AN |
| AD |
解答：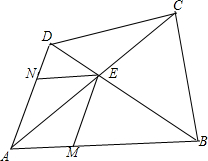
解：过E分别作AB，AD的平行线与AD，AB分别交于N，M点如下图．
∴EM∥AD，EN∥AB
∴四边形AMEN为平行四边形
∴利用向量加法的平行四边形法则可得
=
+
又∵
=x
+y
∴
+
=x
+y
又∵
与
，
与
共线
∴
=x，
=y
又∵EM∥AD，EN∥AB
∴
=
，
=
∴x+y=
+
=
+
=
=
=1
故答案为1
解：过E分别作AB，AD的平行线与AD，AB分别交于N，M点如下图．∴EM∥AD，EN∥AB
∴四边形AMEN为平行四边形
∴利用向量加法的平行四边形法则可得
| AE |
| AM |
| AN |
又∵
| AE |
| AD |
| AB |
∴
| AM |
| AN |
| AD |
| AB |
又∵
| AM |
| AB |
| AN |
| AD |
∴
| AM |
| AB |
| AN |
| AD |
又∵EM∥AD，EN∥AB
∴
| AM |
| AB |
| DE |
| BD |
| AN |
| AD |
| BE |
| BD |
∴x+y=
| AM |
| AB |
| AN |
| AD |
| DE |
| BD |
| BE |
| BD |
| DE+BE |
| BD |
| BD |
| BD |
故答案为1
点评：本题关键是要利用向量加法的平行四边形法则和平行线分线段成比例性质解题．解题的关键是要构造出以AE为对角线的平行四边形然后利用向量加法的平行四边形法则和共线定理再结合平行线分线段成比例性质即可求解．另外若本题是选择和填空的话可采用特殊图形法即将此四边形看成是平行四边形点E看做中点直接即可得解，这也不失为一种好的方法！
练习册系列答案
相关题目
