题目内容
设函数
，其中a∈R。
（1）若a=1，f(x)的定义域为区间[0，3]，求f(x)的最大值和最小值；
（2）若f(x)的定义域为区间（0，+∞），求a的取值范围，使f(x)在定义域内是单调减函数。
，其中a∈R。（1）若a=1，f(x)的定义域为区间[0，3]，求f(x)的最大值和最小值；
（2）若f(x)的定义域为区间（0，+∞），求a的取值范围，使f(x)在定义域内是单调减函数。
解：
，
设
，则
，
（1）当a=1时，设
，
则
，
又
，
∴
，∴
，
∴f(x)在[0，3]上是增函数，
∴
。
（2）设
，则
，
而
，
∴当a+1＜0，即a＜-1时，有
，∴
，
∴当a＜-1时，f(x)在定义域
内是单调减函数。
练习册系列答案
相关题目
，其中a∈R，m是给定的正整数，且m≥2．如果不等式f（x）＞（x-1）lgm在区间[1，+∞）上有解，则实数a的取值范围是 ．
，其中a∈R，m是给定的正整数，且m≥2，如果不等式f（x）＞（x-1）lgm在区间[1，+∞）有解，则实数a的取值范围是 ．
，其中a∈R，m是给定的正整数，且m≥2，如果不等式f（x）＞（x-1）lgm在区间[1，+∞）有解，则实数a的取值范围是 ．
，其中a∈R，m是给定的正整数，且m≥2，如果不等式f（x）＜（x-2）lgm在区间[1，+∞）上恒成立，则实数a的取值范围是 ．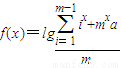
，其中a∈R，m是给定的正整数，且m≥2，如果不等式f（x）＞（x-1）lgm在区间[1，+∞）有解，则实数a的取值范围是 ．