题目内容
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,过左焦点
,过左焦点![]() 且垂直于长轴的弦长为
且垂直于长轴的弦长为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)点![]() 为椭圆
为椭圆![]() 的长轴上的一个动点,过点
的长轴上的一个动点,过点![]() 且斜率为
且斜率为![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点,证明:
两点,证明:![]() 为定值.
为定值.
【答案】(1)![]() (2)详见解析
(2)详见解析
【解析】
试题分析:(1)过左焦点![]() 且垂直于长轴的弦长为通径长,即
且垂直于长轴的弦长为通径长,即![]() ,又离心率为
,又离心率为![]() ,得
,得![]() ,再由
,再由![]() ,解方程组得
,解方程组得![]() (2)解析几何中证明定值问题,一般方法为以算代证,因为
(2)解析几何中证明定值问题,一般方法为以算代证,因为![]() ,利用
,利用![]() ,
,![]() 消y得
消y得![]() ,再联立直线方程
,再联立直线方程![]() 与椭圆方程
与椭圆方程![]() ,结合韦达定理,代入化简得定值41
,结合韦达定理,代入化简得定值41
试题解析:(1)由 ,可得椭圆方程
,可得椭圆方程![]() ..........4分
..........4分
(2)设![]() 的方程为
的方程为![]() ,代入
,代入![]() 并整理得:
并整理得:
![]() .....................6分
.....................6分
设![]() ,则
,则![]() ,
,
又因为![]() ,同理
,同理![]() ..............8分
..............8分
则 ,
,
所以![]() 是定值.................................12分
是定值.................................12分

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】某学校课题组为了研究学生的数学成绩与学生细心程度的关系,在本校随机调查了100名学生进行研究.研究结果表明:在数学成绩及格的60名学生中有45人比较细心,另外15人比较粗心;在数学成绩不及格的40名学生中有10人比较细心,另外30人比较粗心.
(1)试根据上述数据完成![]() 列联表;
列联表;
数学成绩及格 | 数学成绩不及格 | 合计 | |
比较细心 | 45 | ||
比较粗心 | |||
合计 | 60 | 100 |
(2)能否在犯错误的概率不超过0.001的前提下认为学生的数学成绩与细心程度有关系?
参考数据:独立检验随机变量![]() 的临界值参考表:
的临界值参考表:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
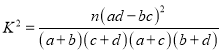 ,其中
,其中![]()