题目内容
在△ABC中,已知tanB=
,sinC=
,AC=3
,则△ABC的面积为
| 3 |
2
| ||
| 3 |
| 6 |
8
±6
| 3 |
| 2 |
8
±6
.| 3 |
| 2 |
分析:要求三角形的面积,根据面积公式,需要求出AB的长及A的正弦值,利用正弦定理,可以解得.
解答:解:由题意tanB=
,得sinB=
,∴cosB=
,
∵sinC=
,
∴cosC=±
=±
∴sinA=sin(B+C)=sinBcosC+cosBsinC=±
×
+
×
=
由正弦定理可得,
=
,∴AB=8.
∴当sinA=
时,△ABC的面积为:
×3
×8×
=8
+6
当sinA=
时,△ABC的面积为:
×3
×8×
=8
-6
故答案为:8
±6
| 3 |
| ||
| 2 |
| 1 |
| 2 |
∵sinC=
2
| ||
| 3 |
∴cosC=±
1-(
|
| 1 |
| 3 |
∴sinA=sin(B+C)=sinBcosC+cosBsinC=±
| ||
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
2
| ||
| 3 |
2
| ||||
| 6 |
由正弦定理可得,
| AC |
| sinB |
| AB |
| sinC |
∴当sinA=
2
| ||||
| 6 |
| 1 |
| 2 |
| 6 |
2
| ||||
| 6 |
| 3 |
| 2 |
当sinA=
2
| ||||
| 6 |
| 1 |
| 2 |
| 6 |
2
| ||||
| 6 |
| 3 |
| 2 |
故答案为:8
| 3 |
| 2 |
点评:本题考查解三角形,正弦定理以及三角形的面积公式,解题的关键是利用正弦定理求出边AB.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 )
) ,H是△ABC的垂心,且
,H是△ABC的垂心,且 .
. 的直线与轨迹M交于点P,点Q(t,0)是x轴上任意一点,求当△CPQ为锐角三角形时t的取值范围.
的直线与轨迹M交于点P,点Q(t,0)是x轴上任意一点,求当△CPQ为锐角三角形时t的取值范围.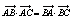 .
. |=|
|=| |;
|; ,求|
,求| -t
-t