题目内容
设集合Pn={1,2,…,n},n∈N*,记f(n)为同时满足下列条件的集合A的个数:①A⊆Pn②若x∈A,则2x∉A③若x∈CPnA,则2x∉CPnA,则f(4)=
4
4
.分析:由题意得P4={1,2,3,4},根据题中的3个条件,可得A的元素满足条件:元素“1”与“4”必须同时属于A,或同时不属于A;元素“2”不能与“1”或“4”同时属于A,或同时不属于A;元素“3”可以属于A也可以不属于A.由此加以分类,可得本题答案.
解答:解:当n=4时,得P4={1,2,3,4},
①若1∈A,则2∉A,即2∈CP4A,可得4∉CP4A,即4∈A,
可得含有元素“1”的集合为A={1,4}或A={1,3,4};
②若1∉A,即1∈CP4A,可得2∉CP4A,即2∈A,同时4∉A,
可得不含有元素“1”的集合为A={2}或A={2,3}.
综上所述,同时满足3个条件的集合A为{1,4}、{1,3,4}、{2}或{2,3},共4个.
由此可得f(4)=4
故答案为:4
①若1∈A,则2∉A,即2∈CP4A,可得4∉CP4A,即4∈A,
可得含有元素“1”的集合为A={1,4}或A={1,3,4};
②若1∉A,即1∈CP4A,可得2∉CP4A,即2∈A,同时4∉A,
可得不含有元素“1”的集合为A={2}或A={2,3}.
综上所述,同时满足3个条件的集合A为{1,4}、{1,3,4}、{2}或{2,3},共4个.
由此可得f(4)=4
故答案为:4
点评:本题给出实际问题,求满足条件的集合的个数.考查了确定集合的元素的知识点,属于中档题.其中分类讨论、确定元素的逻辑关系,然后列举满足条件的集合A是解答的关键.

练习册系列答案
相关题目
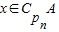 ,则
,则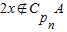 .
.