题目内容
已知两点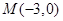 ,
,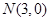 ,点P为坐标平面内一动点,且
,点P为坐标平面内一动点,且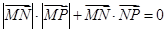 ,则动点
,则动点 到点
到点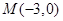 的距离的最小值为( )
的距离的最小值为( )
| A.2 | B.3 | C.4 | D.6 |
B
解析试题分析:设点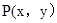 ,因为,
,因为,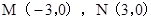 ,
,
所以,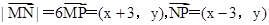 ,
,
由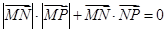 ,得
,得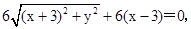 即
即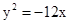 .
.
所以,所以点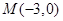 是抛物线
是抛物线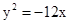 的焦点,动点
的焦点,动点 到点
到点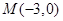 的距离的最小值就是原点到
的距离的最小值就是原点到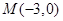 的距离3,故选B.
的距离3,故选B.
考点:平面向量的数量积、坐标运算,抛物线的几何性质.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
已知平面内两个定点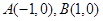 ,过动点
,过动点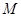 作直线
作直线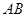 的垂线,垂足为
的垂线,垂足为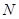 .若
.若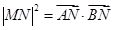 ,则动点
,则动点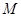 的轨迹是( )
的轨迹是( )
| A.圆 | B.抛物线 | C.椭圆 | D.双曲线 |
已知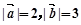 ,
,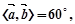
 ,则
,则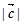 的最小值是( )
的最小值是( )
A.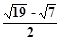 | B.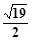 | C.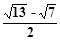 | D.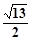 |
在等比数列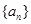 中,
中,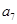 是
是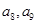 的等差中项,公比
的等差中项,公比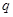 满足如下条件:
满足如下条件: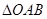 (
(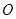 为原点)中,
为原点)中,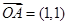 ,
,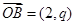 ,
,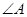 为锐角,则公比
为锐角,则公比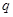 等于( )
等于( )
| A.1 | B.-1 | C.-2 | D.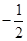 |
已知向量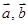 满足:
满足: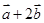 与
与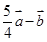 垂直,且
垂直,且 ,则
,则 与
与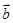 的夹角为( )
的夹角为( )
A.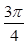 | B.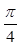 | C.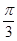 | D.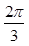 |
已知两不共线向量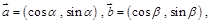 则下列说法不正确的是 ( )
则下列说法不正确的是 ( )
A.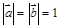 |
B.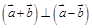 |
C. 与 与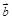 的夹角等于 的夹角等于 |
D. 与 与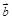 在 在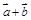 方向上的投影相等 方向上的投影相等 |
已知 是两夹角为120°的单位向量,
是两夹角为120°的单位向量,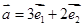 ,则
,则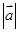 等于( )
等于( )
| A.4 | B.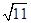 | C.3 | D.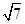 |
在△ABC中,AB=4,AC=3,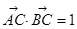 ,则BC=( ).
,则BC=( ).
A.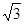 | B.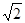 | C.2 | D.3 |
|a|=1,|b|=2,c=a+b,且c⊥a,则向量a与b的夹角为( )
| A.30° | B.60° | C.120° | D.150° |