Question

(1)设等差数列的前n项和为S_n,已知a₃=12,S₁₂＞0,S₁₃＜0,求公差d的取值范围;

(2)指出S₁,S₂,S₃,…,S₁₂中哪一个值最大,并说明理由.

Answer 1

解:(1)S₁₂=12a₁+d＞0,S₁₃=13a₁+d＜0,

    即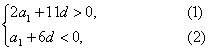

    由a₃=12,得a₁+2d=12,即a₁=12-2d.③

    将③代入①②解不等式组得-＜d＜-3.

(2)由d＜0,可知{a_n}是递减函数,因此在1≤n≤12中,满足a_n≥0且a_n+1＜0的S_n最大,由于S₁₂==6(a₆+a₇)＞0,S₁₃===13a₇＜0.

    因此a₇＜0,a₆＞-a₇＞0,故S₆最大.