题目内容
设![]() ,函数
,函数![]() 。
。
(Ⅰ)求![]() 的单调区间;
的单调区间;
(Ⅱ)若对任意![]() ,不等式
,不等式![]() 恒成立,求a的最大值;
恒成立,求a的最大值;
(Ⅲ)若方程![]() 存在三个相异的实数根,求a的取值范围。
存在三个相异的实数根,求a的取值范围。
(I)解:
![]() ,解得
,解得![]() ,或
,或![]() ;令
;令![]() ,解得
,解得![]() .
.
从而![]() 的单调递增区间为
的单调递增区间为![]() ,
,![]() ;单调递减区间为
;单调递减区间为![]() .
.
…………3分
(II)解:
由![]() . …………4分
. …………4分
由(I)得,函数![]() 在
在![]() ,在
,在![]() 内单调递减,
内单调递减,
从而当![]() 时,函数
时,函数![]() 取得最大值
取得最大值![]() . …………6分
. …………6分
因为对于任意![]() ,不等于
,不等于![]() 恒成立,
恒成立,
故![]() ,即
,即![]() ,
,
从而![]() 的最大值是
的最大值是![]() . …………8分
. …………8分
(III)解:
当![]() 变化时,
变化时,![]() 变化情况如下表:
变化情况如下表:
|
|
|
|
|
|
|
|
| + | 0 | - | 0 | + |
|
|
| 极大值 |
| 极小值 |
|
①由![]() 的单调性,当极大值
的单调性,当极大值![]() 或极小值
或极小值![]() 时,方程
时,方程![]() 最多有一个实数根;
最多有一个实数根;
②当![]() 时,解方程
时,解方程![]() ,得
,得![]() ,即方程
,即方程![]() 只有两个相异的实数根;
只有两个相异的实数根;
③当![]() 时,解方程
时,解方程![]() ,得
,得![]() ,即方程
,即方程![]() 只有两个相异的实数根.
只有两个相异的实数根.
如果方程![]() 存在三个相异的实数根,则
存在三个相异的实数根,则![]()
![]()
 解得
解得![]() .
.
…………12分
事实上,当![]() 时,
时,
![]() ,且
,且![]() ,
,
所以方程![]() 在
在![]() 内各有一根.
内各有一根.
综上,若方程![]() 存在三个相异的实数根,则
存在三个相异的实数根,则![]() 的取值范围是
的取值范围是![]() .……14分
.……14分

练习册系列答案
相关题目
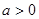 ,函数
,函数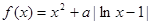
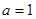 时,求曲线
时,求曲线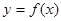 在
在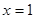 处的切线方程;
处的切线方程;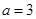 时,求函数
时,求函数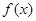 的单调区间;
的单调区间;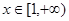 时,求函数
时,求函数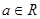 ,函数
,函数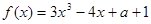 ,
, 的单调区间;
的单调区间;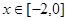 ,不等式
,不等式 恒成立,求
恒成立,求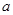 的取值范围。
的取值范围。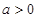 ,函数
,函数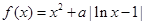 .
. 时,求函数
时,求函数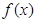 的单调增区间;
的单调增区间; 时,不等式
时,不等式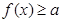 恒成立,实数
恒成立,实数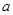 的取值范围.
的取值范围.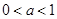 ,函数
,函数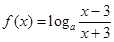 .
.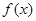 的定义域,并判断
的定义域,并判断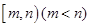 时,值域为
时,值域为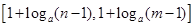 ,求
,求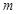 、
、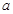 的取值范围.
的取值范围.