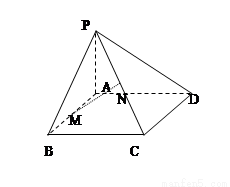题目内容
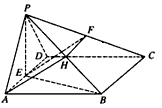
在四棱锥P- ABCD中,平面PAD⊥平面ABCD,△PAD是等边三角形,底面ABCD是边长为2的菱形,∠BAD=60°,E是AD的中点,F是PC的中点,
(Ⅰ)求证:BE⊥平面PAD;
(Ⅱ)求证:EF∥平面PAB;
(Ⅲ)求直线EF与平面PBE所成角的余弦值.
(Ⅰ)求证:BE⊥平面PAD;
(Ⅱ)求证:EF∥平面PAB;
(Ⅲ)求直线EF与平面PBE所成角的余弦值.
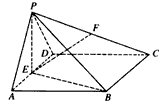
| (Ⅰ)证明:∵E是AD的中点,连结PE, ∴AB=2,AE=1, BE2=AB2+AE2-2AB·AE·cos∠BAD=4+1-2×2×1×cos60°=3, ∴AE2+BE2=1+3=4=AB2, ∴BE⊥AE, 又平面PAD⊥平面ABCD,交线为AD, ∴BE⊥平面PAD. (Ⅱ)证明:取PB中点为H,连接FH,AH, ∵  ,又因为HF是△PBC的中位线, ,又因为HF是△PBC的中位线,∴ 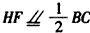 ,∴ ,∴ , ,∴AHFE是平行四边形, ∴EF∥AH, 又 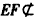 平面PAB,AH 平面PAB,AH 平面PAB, 平面PAB,∴EF∥平面PAB。 (Ⅲ)解:由(Ⅰ)知,BC⊥BE,PE⊥BC, 又PE,BE是平面PBE内两相交直线, ∴BC⊥平面PBE,又由(Ⅱ)知,HF∥BC, ∴FH⊥平面PBE, ∴∠FEH是直线EF与平面PBE所成的角, 易知, 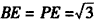 , ,在Rt△PEB中, 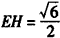 , ,∴ 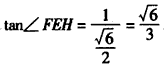 ,∴ ,∴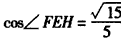 , ,故直线EF与平面PBE所成角的余弦值为 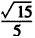 。 。 |
 |

练习册系列答案
相关题目
 (2012•武汉模拟)如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,且AD∥BC,∠ABC=90°,侧棱PA⊥底面ABCD,若AB=BC=
(2012•武汉模拟)如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,且AD∥BC,∠ABC=90°,侧棱PA⊥底面ABCD,若AB=BC= (2012•河南模拟)如图,在四棱锥P-ABCD中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,PA⊥平面ABCD,E为PD的中点,AB=1,PA=2.
(2012•河南模拟)如图,在四棱锥P-ABCD中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,PA⊥平面ABCD,E为PD的中点,AB=1,PA=2.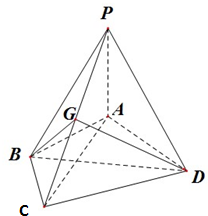 如图,在四棱锥P-ABCD中,PA⊥面ABCD,AB=BC=2,AD=CD=
如图,在四棱锥P-ABCD中,PA⊥面ABCD,AB=BC=2,AD=CD=
 平面ABCD,M,N分别是AB,PC的中点。
平面ABCD,M,N分别是AB,PC的中点。