题目内容
 四边形ABCD是正方形,MD⊥平面ABCD,NB⊥平面ABCD,且MD=NB=AB.则二面角A-MN-C的余弦值为( )
四边形ABCD是正方形,MD⊥平面ABCD,NB⊥平面ABCD,且MD=NB=AB.则二面角A-MN-C的余弦值为( )分析:由已知可将几何体补成正方体ABCD-ENFM,设正方体ABCD-ENFM的边长为1,则
=(-1,-1,1)为平面AMN的一个法向量,
=(1,1,1)为平面CMN的一个法向量,锐二面角A-MN-C的余弦值即为两个法向量夹角余弦值的绝对值.
| CE |
| AF |
解答:解:∵四边形ABCD是正方形,MD⊥平面ABCD,NB⊥平面ABCD,且MD=NB=AB.
将已知的几何体补成正方体ABCD-ENFM,如图所示:
设正方体ABCD-ENFM的边长为1,
以A为坐标原点,AB,AD,AE方向分别为x,y,z轴正方向建立空间坐标系
易得
=(-1,-1,1)为平面AMN的一个法向量,
=(1,1,1)为平面CMN的一个法向量,
设二面角A-MN-C的夹角为θ
则cosθ=
=
故选C
将已知的几何体补成正方体ABCD-ENFM,如图所示:

设正方体ABCD-ENFM的边长为1,
以A为坐标原点,AB,AD,AE方向分别为x,y,z轴正方向建立空间坐标系
易得
| CE |
| AF |
设二面角A-MN-C的夹角为θ
则cosθ=
|
| ||||
|
|
| 1 |
| 3 |
故选C
点评:本题考查的知识点是二面角的平面角及求法,其中将几何体补成正方体ABCD-ENFM,并建立空间坐标系,将二面角问题转化为向量夹角是解答的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 中,E、F分别是
中,E、F分别是 、
、 的中点,G是正方形
的中点,G是正方形 的中心,画出空间四边形AEFG在该正方体的面上的正方向的平行投影的图形.
的中心,画出空间四边形AEFG在该正方体的面上的正方向的平行投影的图形.

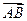 =4i-2j,
=4i-2j,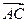 =7i+4j,
=7i+4j,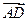 =3i+6j,求四边形ABCD的面积.
=3i+6j,求四边形ABCD的面积.