题目内容
(1)已知 ,
,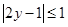 ,求证:
,求证: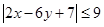 ;
;
(2)已知正数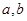 满足关系
满足关系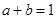 ,求证:
,求证: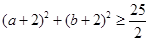 .
.
【答案】
(1)根据两个数和差的绝对值大于等于绝对值的差,小于等于绝对值的和来得到证明。
(2)根据已知中两个正数和为定值,那么将所求的左侧运用配方法的思想来得到和与积的关系,借助于均值不等式得到证明。
【解析】
试题分析:
解:(1) ;6分
;6分
(2)因为正数 满足关系
满足关系
 12分
12分
考点:绝对值不等式,均值不等式
点评:解决的关键是利用放缩法思想,以及均值不等式来构造定值求解最值的思想证明,属于基础题。

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
 ,求证:
,求证: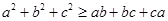 ;
;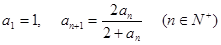 ,写出
,写出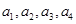 并猜想这个数列的通项公式达式.
并猜想这个数列的通项公式达式.