题目内容
(12分)已知函数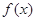 的定义域为
的定义域为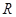 ,对于任意的
,对于任意的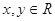 ,都有
,都有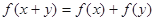 ,且当
,且当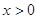 时,
时,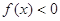 .
.
(1)求证: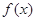 为奇函数; (2)求证:
为奇函数; (2)求证: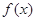 是
是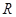 上的减函数;
上的减函数;
【答案】
(1)证明函数的 奇偶性,第一看定义域,第二看解析式,如果两点都满足了,则可以说明结论。
(2)而对于函数单调性的证明主要是结合定义法,作差 ,变形定号,下结论,得到结果,注意最后要化到最简。
【解析】
试题分析:(1)证明: 的定义域为
的定义域为 ,令
,令 ,则
,则 ,
,  令
令 ,则
,则 ,即
,即 .
.
 ,故
,故 为奇函数.
6分
为奇函数.
6分
(2)证明:任取 且
且 ,
,
则
又 ,
, ,
, ,
,
即 .
.
故 是
是 上的减函数. 12分
上的减函数. 12分
考点:函数的奇偶性和单调性
点评:解决该试题的关键是对于函数奇偶性和单调性的运用,属于基础题,利用定义法来证明是常用的方法之一。

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
已知函数 的定义域为
的定义域为 ,部分对应值如下表。
,部分对应值如下表。 的导函数
的导函数 的图像如图所示。
的图像如图所示。
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|

下列关于函数 的命题:
的命题:
①函数 在
在 上是减函数;②如果当
上是减函数;②如果当 时,
时, 最大值是
最大值是 ,那么
,那么 的最大值为
的最大值为 ;③函数
;③函数 有
有 个零点,则
个零点,则 ;④已知
;④已知 是
是 的一个单调递减区间,则
的一个单调递减区间,则 的最大值为
的最大值为 。
。
其中真命题的个数是( )
A、4个 B、3个 C、2个 D、1个
 的定义域为
的定义域为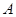 ,
,  ,且
,且 的真子集,求实数
的真子集,求实数 的取值范围.
的取值范围.




 的定义域为
的定义域为 ,且
,且 ,
, 为
为 ,
, 满足
满足 ,则
,则 的取值范围是
的取值范围是
 B.
B. C.
C. D.
D.