题目内容
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,以坐标原点为极点,
中,以坐标原点为极点, ![]() 轴的非负半轴为极轴建立极坐标系,圆
轴的非负半轴为极轴建立极坐标系,圆![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求出圆![]() 的直角坐标方程;
的直角坐标方程;
(2)已知圆![]() 与
与![]() 轴相交于
轴相交于![]() ,
, ![]() 两点,直线
两点,直线![]() :
: ![]() 关于点
关于点![]() 对称的直线为
对称的直线为![]() .若直线
.若直线![]() 上存在点
上存在点![]() 使得
使得![]() ,求实数
,求实数![]() 的最大值.
的最大值.
【答案】(1)![]() 的标准方程为
的标准方程为![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)利用极值互化公式,可得![]() 的标准方程为
的标准方程为![]() .
.
(2)由题可得![]() 是直线
是直线![]() 和以
和以![]() 为直径的圆的公共点,转化为直线
为直径的圆的公共点,转化为直线![]() 与圆有公共点求解.
与圆有公共点求解.
试题解析:(1)由![]() 得
得![]() ,即
,即![]() ,即圆
,即圆![]() 的标准方程为
的标准方程为![]() .
.
(2)![]() :
: ![]() 关于点
关于点![]() 的对称直线
的对称直线![]() 的方程为
的方程为![]() ,而
,而![]() 为圆
为圆![]() 的直径,故直线
的直径,故直线![]() 上存在点
上存在点![]() 使得
使得![]() 的充要条件是直线
的充要条件是直线![]() 与圆
与圆![]() 有公共点,故
有公共点,故![]() ,于是,实数
,于是,实数![]() 的最大值为
的最大值为![]() .
.
点晴:本题考查的是极值互化和直线与圆的位置关系.极值互化时要记清公式,第二问中用了转化与化归思想, ![]() 说明点
说明点![]() 在以
在以![]() 为直径的圆上,同时直线
为直径的圆上,同时直线![]() 上存在点
上存在点![]() ,所以
,所以![]() 是直线
是直线![]() 和以
和以![]() 为直径的圆的公共点,即转化为直线
为直径的圆的公共点,即转化为直线![]() 与圆有公共点,所以
与圆有公共点,所以![]() ,即
,即![]() ,得解.
,得解.

练习册系列答案
相关题目
【题目】为了调查“五一”小长假出游选择“有水的地方”是否与性别有关,现从该市“五一”出游旅客中随机抽取500人进行调查,得到如下2×2列联表:(单位:人)
选择“有水的地方” | 不选择“有水的地方” | 合计 | |
男 | 90 | 110 | 200 |
女 | 210 | 90 | 300 |
合计 | 300 | 200 | 500 |
(Ⅰ)据此样本,有多大的把握认为选择“有水的地方”与性别有关;
(Ⅱ)若以样本中各事件的频率作为概率估计全市“五一”所有出游旅客情况,现从该市的全体出游旅客(人数众多)中随机抽取3人,设3人中选择“有水的地方”的人数为随机变量X,求随机变量X的数学期望和方差.
附临界值表及参考公式:
P(K2≥k0) | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
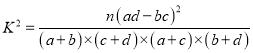 ,n=a+b+c+d.
,n=a+b+c+d.