题目内容
【题目】已知函数f(x)=Asin( ![]() x+φ),x∈R,A>0,0<φ<
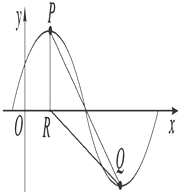
x+φ),x∈R,A>0,0<φ< ![]() .y=f(x)的部分图象如图所示,P、Q 分别为该图象的最高点和最低点,点P的坐标为(1,A).点R的坐标为(1,0),∠PRQ=
.y=f(x)的部分图象如图所示,P、Q 分别为该图象的最高点和最低点,点P的坐标为(1,A).点R的坐标为(1,0),∠PRQ= ![]() .
. 
(1)求f(x)的最小正周期以及解析式.
(2)用五点法画出f(x)在x∈[﹣ ![]() ,
, ![]() ]上的图象.
]上的图象.
【答案】
(1)解:由题意得:f(x)的最小正周期 ![]() ,
,
因为P(1,A)在 ![]() 的图象上,
的图象上,
所以 ![]() ,
,
所以 ![]() ,即
,即 ![]() ,
,
又因为 ![]() ,
,
因此, ![]()
过Q做QD⊥x轴,垂足为D,设D(x0,0),则Q(x0,﹣A),由周期为6可知,RD=3,
由于 ![]() ,
,
所以 ![]() ,于是QD=RD=3,
,于是QD=RD=3,
所以A=3,
∴ ![]()
(2)解:列表如下:
x | ﹣0.5 | 1 | 2.5 | 4 | 5.5 |
| 0 |
| π |
| 2π |
| 0 | 3 | 0 | ﹣3 | 0 |
描点连线,作图如下:
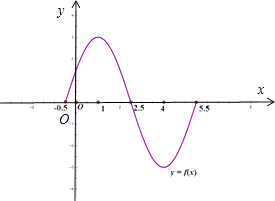
【解析】(1)根据周期公式求出函数f(x)的最小正周期,由P(1,A)在 ![]() 的图象上,结合范围0<φ<
的图象上,结合范围0<φ< ![]() ,可求φ,由图象和条件设出点Q的坐标,再过点Q做x轴的垂线,设垂足为D,根据条件和正切函数求出A,从而可得函数解析式;(2)利用五点作图法即可作图得解.
,可求φ,由图象和条件设出点Q的坐标,再过点Q做x轴的垂线,设垂足为D,根据条件和正切函数求出A,从而可得函数解析式;(2)利用五点作图法即可作图得解.
【考点精析】认真审题,首先需要了解五点法作函数y=Asin(ωx+φ)的图象(描点法及其特例—五点作图法(正、余弦曲线),三点二线作图法(正、余切曲线)).

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目