题目内容
在平面直角坐标系xOy中,△ABC的顶点B、C的坐标为B(-2,0),C(2,0),直线AB,AC的斜率乘积为 ,设顶点A的轨迹为曲线E.
,设顶点A的轨迹为曲线E.
(1)求曲线E的方程;
(2)设曲线E与y轴负半轴的交点为D,过点D作两条互相垂直的直线l1,l2,这两条直线与曲线E的另一个交点分别为M,N.设l1的斜率为k(k≠0),△DMN的面积为S,试求 的取值范围.
的取值范围.
 ,设顶点A的轨迹为曲线E.
,设顶点A的轨迹为曲线E.(1)求曲线E的方程;
(2)设曲线E与y轴负半轴的交点为D,过点D作两条互相垂直的直线l1,l2,这两条直线与曲线E的另一个交点分别为M,N.设l1的斜率为k(k≠0),△DMN的面积为S,试求
 的取值范围.
的取值范围.(1)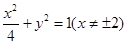 ;(2)
;(2)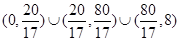
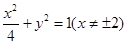 ;(2)
;(2)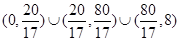
试题分析:(1)由于所求动点A满足直线AB,AC的斜率乘积为
 ,所以直接设A的坐标,代入化简整理即得:
,所以直接设A的坐标,代入化简整理即得: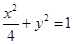 ,注意到△ABC中三个顶点不能共线,所以需去掉与
,注意到△ABC中三个顶点不能共线,所以需去掉与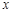 轴相交的点,(2)要求
轴相交的点,(2)要求 的取值范围,首先求出
的取值范围,首先求出 函数解析式,由题意确定l1的斜率为k为自变量,因为M 为l1与曲线E的交点,所以列方程组解出点M坐标
函数解析式,由题意确定l1的斜率为k为自变量,因为M 为l1与曲线E的交点,所以列方程组解出点M坐标 ,从而得出弦长
,从而得出弦长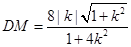 ;同理,只需将
;同理,只需将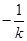 代k就可得到
代k就可得到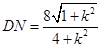 ,因此△DMN的面积S=
,因此△DMN的面积S=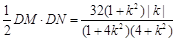 ,所以
,所以 =
= ,这可以看作关于1+k2的一个分式函数,即
,这可以看作关于1+k2的一个分式函数,即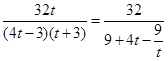 ,可以利用函数单调性求出其取值范围.
,可以利用函数单调性求出其取值范围.试题解析:解(1)设顶点A的坐标为(x,y),则kAB=
 ,kAC=
,kAC= 2分
2分因为kAB×kAC=
 ,所以
,所以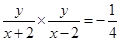 , 即
, 即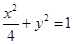 .(或x2+4y2=4).
.(或x2+4y2=4).所以曲线E的方程为
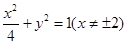 . 4分
. 4分(2)曲线E与y轴负半轴的交点为D(0,-1).
因为l1的斜率存在,所以设l1的方程为y=kx-1, 代入
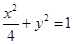 ,得
,得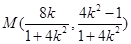
从而
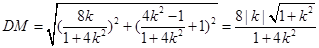 6分
6分用
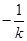 代k得
代k得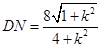
所以△DMN的面积S=
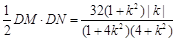 8分
8分则
 =
= 
因为k≠0且
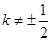 ,k≠±2,令1+k2=t,
,k≠±2,令1+k2=t,则t>1,且
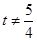 ,t≠5,
,t≠5,从而
 =
= 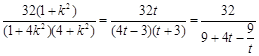
因为
 ,且
,且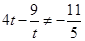 ,
,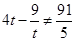
所以
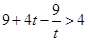 且
且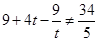 ,
,
从而
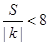 且
且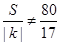 ,
,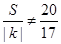 ,
,即
 ∈
∈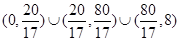 10分.
10分.
练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
 、
、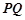 的四个端点都在椭圆
的四个端点都在椭圆 上,其中,直线
上,其中,直线 ,直线
,直线 .
.
 ,
, ,求
,求 的值;
的值; 变化时,恒有
变化时,恒有 的直线l与椭圆
的直线l与椭圆 =1(a>b>0)有两个不同的交点,且这两个交点在x轴上的射影恰好是椭圆的两个焦点,则该椭圆的离心率为________.
=1(a>b>0)有两个不同的交点,且这两个交点在x轴上的射影恰好是椭圆的两个焦点,则该椭圆的离心率为________. =1的焦距为2,求椭圆上的一点到两个焦点的距离之和.
=1的焦距为2,求椭圆上的一点到两个焦点的距离之和. 的焦距为4,那么
的焦距为4,那么 的值为( )
的值为( )
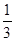


 的左顶点A的斜率为k的直线交椭圆C于另一个点
的左顶点A的斜率为k的直线交椭圆C于另一个点 ,且点
,且点 轴上的射影恰好为右焦点
轴上的射影恰好为右焦点 ,若
,若 则椭圆离心率的取值范围是( )
则椭圆离心率的取值范围是( )

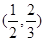

 的焦距为2,则m的取值是 ( )
的焦距为2,则m的取值是 ( ) +
+ =1(a>0,b>0)的右焦点为F(3,0),且点(-3,
=1(a>0,b>0)的右焦点为F(3,0),且点(-3,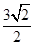 )在椭圆C上,则椭圆C的标准方程为 .
)在椭圆C上,则椭圆C的标准方程为 . =
=
 .
.