题目内容
12．过直线A1x+B1y+C1=0和A2x+B2y+C2=0的交点的直线方程可设为A1x+B1y+C1+λ（A2x+B2y+C2）=0（λ∈R）．分析 设（x1，y1）是直线l1与l2交点，经过推理可得（x1，y1）是直线方程A1x+B1y+C1+λ（A2x+B2y+C2）=0（λ∈R）上的点即可．
解答 解：设（x1，y1）是直线l1：A1x+B1y+C1=0与l2：A2x+B2y+C2=0的交点，
则A1x1+B1y1+C1=0，且A2x1+B2y1+C2=0
∴A1x1+B1y1+C1+λ（A2x1+B2y1+C2）=0，（λ∈R）
∴（x1，y1）也是直线A1x+B1y+C1+λ（A2x+B2y+C2）=0（λ∈R）上的点．
∴A1x+B1y+C1+λ（A2x+B2y+C2）=0（λ∈R）是表示过l1与l2交点的直线方程．
故答案为：A1x+B1y+C1+λ（A2x+B2y+C2）=0（λ∈R）．
点评 本题考查了求过两条直线交点的直线分析的应用问题，是基础题目．
练习册系列答案
相关题目
20．函数f（x）=$\frac{\sqrt{4-{x}^{2}}}{4-|x-4|}$是（ ）
| A． | 奇函数但不是偶函数 | B． | 偶函数但不是奇函数 | ||
| C． | 既是奇函数又是偶函数 | D． | 既不是奇函数又不是偶函数 |
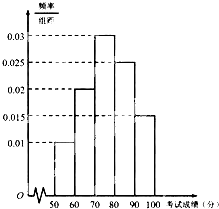某市为了了解本市高中学生的汉字书写水平，在全市范围内随机抽取了近千名学生参加汉字听写考试，将所得数据整理后，绘制出频率分布直方图如图所示，其中样本数据分组区间为[50，60），[60，70），[70，80），[80，90），[90，100]．