题目内容
已知直四棱柱AC1的底面是一个菱形，AB=6，∠BAD=60°，侧棱AA1=12，E是AA1的中点，求：(1)截面BDE与截面BDC1的面积；
(2)二面角EBDC的大小；
(3)A点到平面BDE的距离.
解析：(1)如图，连结AC交BD于点O，?
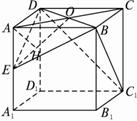
∵底面ABCD是菱形，且∠BAD=60°，∴BD=6.连结OE.?
∵AE=
AA1=6,AE⊥AC,AO=
AC=
,?
∴
.?
∵OE⊥BD,∴
.?
(2)∵BD⊥OE,BD⊥AC,?
∴∠COE为二面角E-BD-C的平面角.?
在Rt△AOE中，
.?
∴∠AOE=arctan
.?
∴∠COE=π-arctan
,?
即二面角EBDC的大小为π-arctan
.?
(3)过A作AH⊥EO交EO于点H，?
∵BD⊥AC,由三垂线定理得BD⊥AH,?
∴AH⊥平面EBD.
? ∴AH为点A到平面BDE的距离.?
∴
,?
即点A到平面BDE的距离为
.
练习册系列答案
相关题目
已知直四棱柱ABCD-A1B1C1D1的底面是菱形，且∠DAB=60°，AD=AA1，F为棱BB1的中点，M为线段AC1的中点．
已知直四棱柱ABCD-A1B1C1D1的底面是菱形，且∠DAB=60°，AD=AA1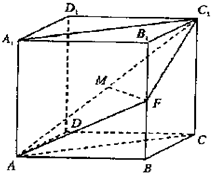，F为棱BB1的中点，M为线段AC1的中点．
已知直四棱柱ABCD-A1B1C1D1的底面是菱形，F为棱BB1的中点，M为线段AC1的中点．