题目内容
在棱长为1的正四面体ABCD中,E,F分别是BC,AD中点,则
•
=( )
| AE |
| CF |
分析:欲求
•
,先把要求数量积的两个向量表示成以四面体的棱所在向量为基底的向量的表示形式,写出向量的数量积,问题转化成四面体的棱向量之间的关系,因为棱长及其夹角可知,从而得到结果.
| AE |
| CF |
解答: 解:
解:
•
=
(
+
)•(
-
)
=
•
+
•
-
•
-
•
=
(1×1×cos60°+1×1×cos60°-2×cos60°-2)
=-
故选D.
 解:
解:| AE |
| CF |
| 1 |
| 2 |
| AB |
| AC |
| 1 |
| 2 |
| AD |
| AC |
=
| 1 |
| 4 |
| AB |
| AD |
| 1 |
| 4 |
| AC |
| AD |
| 1 |
| 2 |
| AB |
| AC |
| 1 |
| 2 |
| AC |
| AC |
=
| 1 |
| 4 |
=-
| 1 |
| 2 |
故选D.
点评:本题考查空间向量的数量积,解题的关键是把要用的向量写成以已知几何体的一个顶点为起点的向量为基地的形式,再进行运算.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
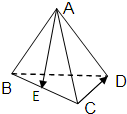 在棱长为1的正四面体ABCD中,E是BC的中点,则
在棱长为1的正四面体ABCD中,E是BC的中点,则 ( )
( ) C、
C、 D、
D、 www..com
高#考#资#源#
www..com
高#考#资#源#