题目内容
(本小题满分12分)
三棱锥被平行于底面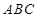 的平面所截得的几何体如图所示,截面为
的平面所截得的几何体如图所示,截面为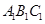 ,
,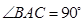 ,
,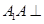
 平面
平面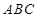 ,
,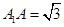 ,
,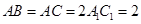 ,
,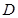 为
为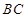 中点.
中点.
(Ⅰ)证明:平面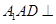 平面
平面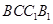 ;
;
(Ⅱ)求二面角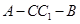 的正弦值.
的正弦值.
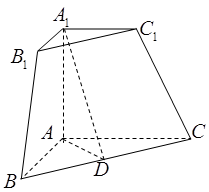
三棱锥被平行于底面
 的平面所截得的几何体如图所示,截面为
的平面所截得的几何体如图所示,截面为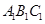 ,
,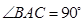 ,
,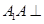
 平面
平面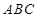 ,
,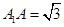 ,
,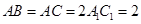 ,
,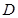 为
为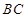 中点.
中点.(Ⅰ)证明:平面
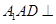 平面
平面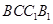 ;
;(Ⅱ)求二面角
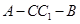 的正弦值.
的正弦值.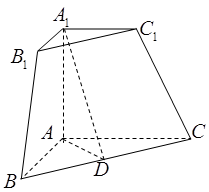
解:(Ⅰ)
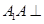 平面
平面 平面
平面 ,
,

在 中,
中, ,
, 为
为 中点
中点
 .
.
 平面
平面 ,
, 平面
平面
 平面
平面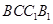 .
.
(Ⅱ)如图,作 交
交 于
于 点,连接
点,连接 ,
,
由 已知得
已知得 平面
平面 .
. 是
是 在面
在面
 内的射影.
内的射影.
由三垂线定理知 ,
, 为二面角
为二面角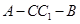 的平面角.
的平面角.
过 作
作 交
交 于
于 点,则
点,则 ,
, ,
,
 .在
.在 中,
中, .
.
在 中,
中, ,
,
即二面角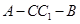 的正弦值是
的正弦值是 。
。

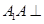 平面
平面 平面
平面 ,
,

在
 中,
中, ,
, 为
为 中点
中点
 .
. 平面
平面 ,
, 平面
平面
 平面
平面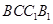 .
.(Ⅱ)如图,作
 交
交 于
于 点,连接
点,连接 ,
,由
 已知得
已知得 平面
平面 .
. 是
是 在面
在面
 内的射影.
内的射影.由三垂线定理知
 ,
, 为二面角
为二面角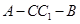 的平面角.
的平面角.过
 作
作 交
交 于
于 点,则
点,则 ,
, ,
, .在
.在 中,
中, .
.在
 中,
中, ,
,
即二面角
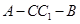 的正弦值是
的正弦值是 。
。略

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目



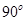
 -
- 中,底面
中,底面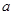 的正方形,
的正方形, 、
、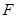 分别为
分别为 、
、 的中点,侧面
的中点,侧面 底面
底面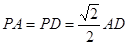 。
。 平面
平面 ;
; 平面
平面 ;
; -
- 的体积。
的体积。
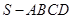 的底面是正方形,每条侧棱的长都是底面边长的
的底面是正方形,每条侧棱的长都是底面边长的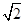 倍,
倍,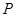 为侧棱
为侧棱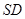 上的点。
上的点。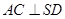 ;
; 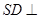 平面
平面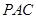 ,求二面角
,求二面角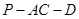 的大小;
的大小;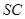 上是否存在一点
上是否存在一点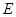 , 使得
, 使得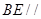 平面
平面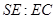 的值;若不存在,试说明理由。
的值;若不存在,试说明理由。
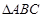 中,
中, ,垂足为
,垂足为 ,且
,且 .
.  的大小;
的大小; 为
为 的中点,已知
的中点,已知 的长
的长 
 和平面
和平面 的命题,其中为真命题的是
的命题,其中为真命题的是  ,则
,则
 与
与 所成的角相等,则
所成的角相等,则 ,则
,则
 ,则
,则
 中,
中,
 平面
平面 ,
, ,
, 是
是 的中点.
的中点. //平面
//平面 ;
; ;
; 使得平面
使得平面

 中,点
中,点 在线段
在线段 上运动时,给出下列四个命题:
上运动时,给出下列四个命题:
 的体积不变;
的体积不变; 与平面
与平面 所成角的大小不变;
所成角的大小不变; 所成角的大小不变;
所成角的大小不变; 的大小不变.
的大小不变.