题目内容
已知函数f(x)=x2-(a+2)x+alnx.其中常数a>0.(1)当a>2时,求函数f(x)的单调递增区间;
(2)当a=4时,给出两类直线:6x+y+m=0与3x-y+n=0,其中m,n为常数,判断这两类直线中是否存在y=f(x)的切线,若存在,求出相应的m或n的值,若不存在,说明理由.
(3)设定义在D上的函数y=h(x)在点P(x,h(x))处的切线方程为l:y=g(x),当x≠x时,若
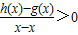 在D内恒成立,则称P为函数y=h(x)的“类对称点”,当a=4时,试问y=f(x)是否存在“类对称点”,若存在,请至少求出一个“类对称点”的横坐标,若不存在,说明理由.
在D内恒成立,则称P为函数y=h(x)的“类对称点”,当a=4时,试问y=f(x)是否存在“类对称点”,若存在,请至少求出一个“类对称点”的横坐标,若不存在,说明理由.
【答案】分析:(1)由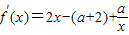 =
=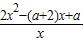 =
=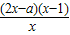 ,能求出当a>2时,求函数f(x)的单调递增区间.
,能求出当a>2时,求函数f(x)的单调递增区间.
(2)a=4,f′(x)=2x+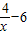 ,故
,故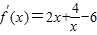 ≥4
≥4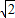 -6,不存在6x+y+m=0这类直线的切线.
-6,不存在6x+y+m=0这类直线的切线.
(3)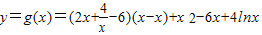 ,令h(x)=f(x)-g(x),由此入手,能够求出一个“类对称点”的横坐标.
,令h(x)=f(x)-g(x),由此入手,能够求出一个“类对称点”的横坐标.
解答:解:(1)∵f(x)=x2-(a+2)x+alnx,
∴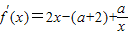 =
=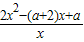 =
=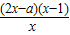 ,
,
∵a>2,∴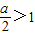 .
.
当0<x<1及x>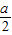 时,f′(x)>0.当1<x<
时,f′(x)>0.当1<x< 时,f′(x)<0,
时,f′(x)<0,
∴f(x)的增区间是(0,1),( ).
).
(2)a=4,f′(x)=2x+ ,
,
∵x>0,∴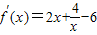 ≥4
≥4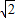 -6,
-6,
不存在6x+y+m=0这类直线的切线.
由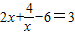 得
得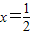 与x=4,当
与x=4,当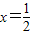 时,求得
时,求得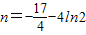 .
.
当x=4时,求得n=4ln4-20.
(3) ,
,
令h(x)=f(x)-g(x)=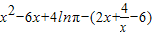 •(x-x)-(
•(x-x)-(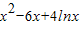 ),
),
则h(x)=0,
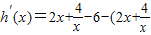 -6)=2(x-x)(1-
-6)=2(x-x)(1-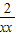 )=
)=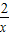 (x-x)(x-
(x-x)(x-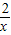 ),
),
当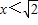 时,h(x)在(x,
时,h(x)在(x,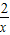 )上单调递减.
)上单调递减.
∴x∈(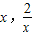 )时,h(x)<h(x)=0,从而有x∈(
)时,h(x)<h(x)=0,从而有x∈(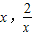 )时,
)时,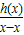 <0,
<0,
当 时,h(x)在(
时,h(x)在(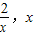 )上单调递减,
)上单调递减,
∴x∈(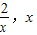 ).
).
h(x)>h(x)=0.从而有 时,
时,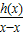 <0.
<0.
∴在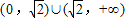 上不存在“类对称点”.
上不存在“类对称点”.
当x=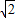 时,
时,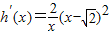 ,
,
∴h(x)在(0,+∞)上是增函数,故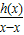 >0,
>0,
x=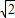 是一个类对称点的横坐标.
是一个类对称点的横坐标.
点评:本题考查函数的单调区间的求法,考查类对称点的求法.解题时要认真审题,注意挖掘题设中的隐含条件,合理地进行等价转化,注意导数性质的灵活运用.
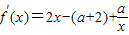 =
=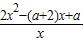 =
=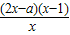 ,能求出当a>2时,求函数f(x)的单调递增区间.
,能求出当a>2时,求函数f(x)的单调递增区间.(2)a=4,f′(x)=2x+
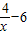 ,故
,故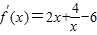 ≥4
≥4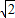 -6,不存在6x+y+m=0这类直线的切线.
-6,不存在6x+y+m=0这类直线的切线.(3)
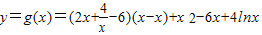 ,令h(x)=f(x)-g(x),由此入手,能够求出一个“类对称点”的横坐标.
,令h(x)=f(x)-g(x),由此入手,能够求出一个“类对称点”的横坐标.解答:解:(1)∵f(x)=x2-(a+2)x+alnx,
∴
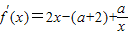 =
=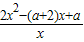 =
=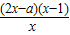 ,
,∵a>2,∴
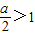 .
.当0<x<1及x>
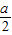 时,f′(x)>0.当1<x<
时,f′(x)>0.当1<x< 时,f′(x)<0,
时,f′(x)<0,∴f(x)的增区间是(0,1),(
 ).
).(2)a=4,f′(x)=2x+
 ,
,∵x>0,∴
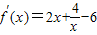 ≥4
≥4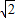 -6,
-6,不存在6x+y+m=0这类直线的切线.
由
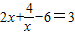 得
得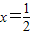 与x=4,当
与x=4,当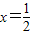 时,求得
时,求得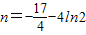 .
.当x=4时,求得n=4ln4-20.
(3)
 ,
,令h(x)=f(x)-g(x)=
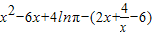 •(x-x)-(
•(x-x)-(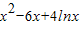 ),
),则h(x)=0,
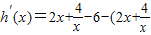 -6)=2(x-x)(1-
-6)=2(x-x)(1-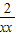 )=
)=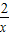 (x-x)(x-
(x-x)(x-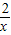 ),
),当
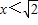 时,h(x)在(x,
时,h(x)在(x,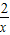 )上单调递减.
)上单调递减.∴x∈(
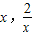 )时,h(x)<h(x)=0,从而有x∈(
)时,h(x)<h(x)=0,从而有x∈(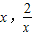 )时,
)时,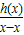 <0,
<0,当
 时,h(x)在(
时,h(x)在(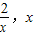 )上单调递减,
)上单调递减,∴x∈(
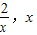 ).
).h(x)>h(x)=0.从而有
 时,
时,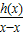 <0.
<0.∴在
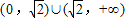 上不存在“类对称点”.
上不存在“类对称点”.当x=
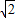 时,
时,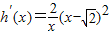 ,
,∴h(x)在(0,+∞)上是增函数,故
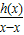 >0,
>0,x=
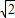 是一个类对称点的横坐标.
是一个类对称点的横坐标.点评:本题考查函数的单调区间的求法,考查类对称点的求法.解题时要认真审题,注意挖掘题设中的隐含条件,合理地进行等价转化,注意导数性质的灵活运用.

练习册系列答案
相关题目
 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<| π |
| 2 |
A、f(x)=2sin(πx+
| ||
B、f(x)=2sin(2πx+
| ||
C、f(x)=2sin(πx+
| ||
D、f(x)=2sin(2πx+
|