题目内容
(14分)设集合W由满足下列两个条件的数列 构成:
构成:
①
②存在实数M,使 (n为正整数)
(n为正整数)
(I)在只有5项的有限数列
 ;试判断数列
;试判断数列 是否为集合W的元素;
是否为集合W的元素;
(II)设 是各项为正的等比数列,
是各项为正的等比数列, 是其前n项和,
是其前n项和, 证明数列
证明数列 ;并写出M的取值范围;
;并写出M的取值范围;
(III)设数列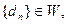 且对满足条件的M的最小值M0,都有
且对满足条件的M的最小值M0,都有 .
.
求证:数列 单调递增.
单调递增.
(I) 不是集合W中的元素,
不是集合W中的元素, 是集合W中的元素.(II)
是集合W中的元素.(II) ,且
,且 (III)见解析
(III)见解析
解析

练习册系列答案
相关题目
题目内容
(14分)设集合W由满足下列两个条件的数列 构成:
构成:
①
②存在实数M,使 (n为正整数)
(n为正整数)
(I)在只有5项的有限数列
 ;试判断数列
;试判断数列 是否为集合W的元素;
是否为集合W的元素;
(II)设 是各项为正的等比数列,
是各项为正的等比数列, 是其前n项和,
是其前n项和, 证明数列
证明数列 ;并写出M的取值范围;
;并写出M的取值范围;
(III)设数列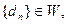 且对满足条件的M的最小值M0,都有
且对满足条件的M的最小值M0,都有 .
.
求证:数列 单调递增.
单调递增.
(I) 不是集合W中的元素,
不是集合W中的元素, 是集合W中的元素.(II)
是集合W中的元素.(II) ,且
,且 (III)见解析
(III)见解析
解析
