题目内容
已知向量
=（sinx，cosx），
=（cosx，-cosx），f（x）=2
+||
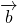（1）写出函数f（x）的解析式
（2）求f（x）的单调区间
（3）若在[0，π]上f（x）=m有两个不同的实根，求实数m的取值范围．
解：（1）f（x）=
=2sinxcosx-2cos2x+
=sin2x-cos2x=
．
（2）由
解得
，（k∈Z）．
∴函数f（x）的单调递增区间为
（k∈Z）．
由
解得
（k∈Z）．
∴函数f（x）的单调递减区间为
（k∈Z）．
（3）由x∈[0，π]，得
，∴
，∴
，
如图所示：
要使f（x）=m在[0，π]上有两个不同的实根，则m取值范围是
．
分析：（1）利用向量的数量积、模的计算公式、三角函数的两角和差、倍角、平方关系等有关公式即可得出；
（2）利用正弦函数的单调性即可得出；
（3）利用三角函数的图象和性质即可求出．
点评：熟练掌握向量的数量积、模的计算公式、三角函数的两角和差、倍角、平方关系等有关公式、正弦函数的单调性、三角函数的图象和性质是解题的关键．
=2sinxcosx-2cos2x+=sin2x-cos2x=．（2）由
解得，（k∈Z）．∴函数f（x）的单调递增区间为
（k∈Z）．由
解得（k∈Z）．∴函数f（x）的单调递减区间为
（k∈Z）．（3）由x∈[0，π]，得
，∴，∴，如图所示：
要使f（x）=m在[0，π]上有两个不同的实根，则m取值范围是
．分析：（1）利用向量的数量积、模的计算公式、三角函数的两角和差、倍角、平方关系等有关公式即可得出；
（2）利用正弦函数的单调性即可得出；
（3）利用三角函数的图象和性质即可求出．
点评：熟练掌握向量的数量积、模的计算公式、三角函数的两角和差、倍角、平方关系等有关公式、正弦函数的单调性、三角函数的图象和性质是解题的关键．
练习册系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
已知向量
=（sinx，cosx），向量
=(1，
)，则|
+
|的最大值为（ ）
| a |
| b |
| 3 |
| a |
| b |
| A、3 | ||
B、
| ||
| C、1 | ||
| D、9 |