题目内容
已知抛物线![]() :
:![]() 和点
和点![]() ,若抛物线
,若抛物线![]() 上存在不同两点
上存在不同两点![]() 、
、![]() 满足
满足![]() .
.
(1)求实数![]() 的取值范围;
的取值范围;
(2)当![]() 时,抛物线
时,抛物线![]() 上是否存在异于
上是否存在异于![]() 、
、![]() 的点
的点![]() ,使得经过
,使得经过![]() 、
、![]() 、
、![]() 三点的圆和抛物线
三点的圆和抛物线![]() 在点
在点![]() 处有相同的切线,若存在,求出点
处有相同的切线,若存在,求出点![]() 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.
(本小题主要考查直线与圆锥曲线等基础知识,考查数形结合的数学思想方法,以及推理论证能力.运算求解能力)
解法1:(1)不妨设A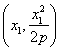 ,B
,B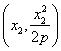 ,且
,且![]() , ∵
, ∵![]() ,∴
,∴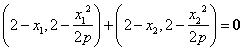 .
.
∴![]() ,
,![]() .…………………4分
.…………………4分
∵![]() (
(![]() ),即
),即![]() ,
,
∴![]() ,即
,即![]() 的取值范围为
的取值范围为![]() .…………………6分
.…………………6分
(2)当![]() 时,由(1)求得
时,由(1)求得![]() .
.![]() 的坐标分别为
的坐标分别为![]() .
.![]() .
.
假设抛物线![]() 上存在点
上存在点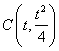 (
(![]() 且
且![]() ),…………8分
),…………8分
使得经过![]() .
.![]() .
.![]() 三点的圆和抛物线
三点的圆和抛物线![]() 在点
在点![]() 处有相同的切线.
处有相同的切线.
设经过![]() .
.![]() .
.![]() 三点的圆的方程为
三点的圆的方程为![]() ,
,
则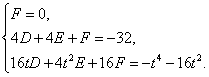
整理得 ![]() . ①…………9分
. ①…………9分
∵函数![]() 的导数为
的导数为![]() ,
,
∴抛物线![]() 在点
在点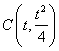 处的切线的斜率为
处的切线的斜率为![]() ,
,
∴经过![]() .
.![]() .
.![]() 三点的圆
三点的圆![]() 在点
在点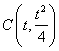 处的切线 斜率为
处的切线 斜率为![]() .………10分
.………10分
∵![]() ,∴直线
,∴直线![]() 的斜率存在.
的斜率存在.
∵圆心![]() 的坐标为
的坐标为![]() ,
,
∴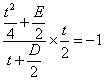 ,
,
即![]() . ②…………………12分
. ②…………………12分
∵![]() ,由①.②消去
,由①.②消去![]() ,得
,得![]() .
.
即![]() .
.
∵![]() ,∴
,∴![]() .
.
故满足题设的点![]() 存在,其坐标为
存在,其坐标为![]() .…………………14分
.…………………14分
解法2:(1)设![]() ,
,![]() 两点的坐标为
两点的坐标为![]() ,且
,且![]() 。
。
∵![]() ,可得
,可得![]() 为
为![]() 的中点,
的中点,
即![]() .…………………2分
.…………………2分
显然直线![]() 与
与![]() 轴不垂直,
轴不垂直,
设直线![]() 的方程为
的方程为![]() , 即
, 即![]() ,…………………3分
,…………………3分
将![]() 代入
代入![]() 中,
中,
得![]() . …………………4分
. …………………4分
∴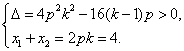 ∴
∴![]() .
.
故![]() 的取值范围为
的取值范围为![]() . …………………6分
. …………………6分
(2)当![]() 时,由(1)求得
时,由(1)求得![]() ,
,![]() 的坐标分别为
的坐标分别为![]() .
.
假设抛物线![]() 上存在点
上存在点 (
(![]() 且
且![]() ),
),
使得经过![]() .
.![]() .
.![]() 三点的圆和抛物线
三点的圆和抛物线![]() 在点
在点![]() 处有相同的切线.
处有相同的切线.
设圆的圆心坐标为![]()
![]() ,
,
∵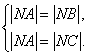
∴ 即
即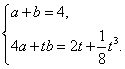 …………………8分
…………………8分
解得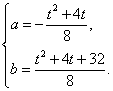 …………………10分
…………………10分
∵抛物线![]() 在点
在点![]() 处切线的斜率为
处切线的斜率为![]() ,
,
而![]() ,且该切线与
,且该切线与![]() 垂直,∴
垂直,∴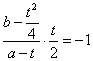 .
.
即![]() . …………………12分
. …………………12分
将![]() ,
,![]() 代入上式,
代入上式,
得![]() .
.
即![]() . ∵
. ∵![]() 且
且![]() ,∴
,∴![]() .
.
故满足题设的点![]() 存在,其坐标为
存在,其坐标为 ![]() . …………………14分
. …………………14分

 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案 :
: 和⊙
和⊙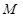 :
: ,过抛物线
,过抛物线 作两条直线与⊙
作两条直线与⊙ 相切于
相切于 、
、 两点,分别交抛物线为E、F两点,圆心点
两点,分别交抛物线为E、F两点,圆心点 .
.
 的方程;
的方程; 的角平分线垂直
的角平分线垂直 轴时,求直线
轴时,求直线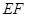 的斜率;
的斜率; 在
在 轴上的截距为,求的最小值.
轴上的截距为,求的最小值. :
: 和⊙
和⊙ :
: ,过抛物线
,过抛物线 作两条直线与⊙
作两条直线与⊙ 、
、 两点,分别交抛物线为E、F两点,圆心点
两点,分别交抛物线为E、F两点,圆心点 .
.
 的角平分线垂直轴时,求直线
的角平分线垂直轴时,求直线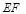 的斜率;
的斜率; 在
在 轴上的截距为,求的最小值.
轴上的截距为,求的最小值. :
: 和点
和点 ,若抛物线
,若抛物线 、
、 满足
满足 .
. 的取值范围;
的取值范围; 时,抛物线
时,抛物线 的点
的点 ,使得经过
,使得经过 三点的圆和抛物线
三点的圆和抛物线 :
: 和⊙
和⊙ :
: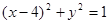 ,过抛物线
,过抛物线 作两条直线与⊙
作两条直线与⊙ 、
、 两点,分别交抛物线于
两点,分别交抛物线于 两点,圆心点
两点,圆心点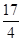 .
.
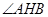 的角平分线垂直
的角平分线垂直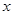 轴时,求直线
轴时,求直线 的斜率;
的斜率; 在
在 轴上的截距为
轴上的截距为 ,求
,求