题目内容
(本小题满分12分)已知抛物线 :
: 和点
和点 ,若抛物线
,若抛物线 上存在不同两点
上存在不同两点 、
、 满足
满足 .
.
(I)求实数 的取值范围;
的取值范围;
(II)当 时,抛物线
时,抛物线 上是否存在异于
上是否存在异于 的点
的点 ,使得经过
,使得经过 三点的圆和抛物线
三点的圆和抛物线 在点
在点 处有相同的切线,若存在,求出点
处有相同的切线,若存在,求出点 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.
(1) 即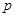 的取值范围为
的取值范围为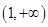 .
.
(2) 满足题设的点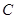 存在,其坐标为
存在,其坐标为 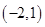 .
.
【解析】
试题分析:解法1:(I)不妨设A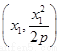 ,B
,B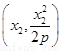 ,且
,且 ,∵
,∵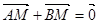 ,
,
∴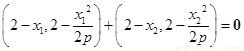 .∴
.∴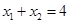 ,
,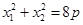 .
.
根据基本不等式 (当且仅当
(当且仅当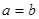 时取等号)得
时取等号)得
 (
(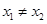 ),即
),即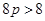 ,
,
∴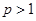 ,即
,即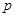 的取值范围为
的取值范围为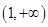 .
.
(II)当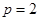 时,由(I求得
时,由(I求得 、
、 的坐标分别为
的坐标分别为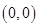 、
、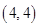 .
.
假设抛物线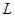 上存在点
上存在点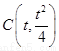 (
(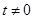 ,且
,且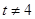 ),使得经过
),使得经过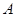 、
、 、
、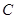 三点的圆和抛物线
三点的圆和抛物线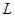 在点
在点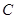 处有相同的切线.
处有相同的切线.
设经过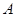 、
、 、
、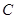 三点的圆的方程为
三点的圆的方程为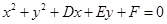 ,
,
则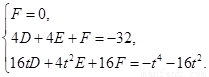
整理得  . ①
. ①
∵函数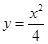 的导数为
的导数为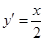 ,
,
∴抛物线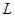 在点
在点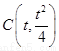 处的切线的斜率为
处的切线的斜率为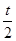 ,
,
∴经过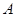 、
、 、
、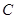 三点的圆
三点的圆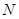 在点
在点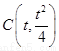 处的切线斜率为
处的切线斜率为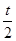 .
.
∵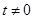 ,∴直线
,∴直线 的斜率存在.∵圆心
的斜率存在.∵圆心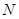 的坐标为
的坐标为 ,
,
∴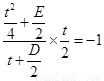 ,即
,即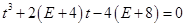 . ②
. ②
∵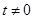 ,由①、②消去
,由①、②消去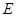 ,得
,得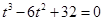 . 即
. 即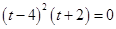 .
.
∵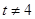 ,∴
,∴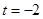 .故满足题设的点
.故满足题设的点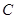 存在,其坐标为
存在,其坐标为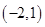 .
.
解法2:(I)设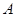 ,
,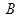 两点的坐标为
两点的坐标为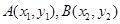 ,且
,且 。
。
∵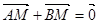 ,可得
,可得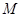 为
为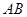 的中点,即
的中点,即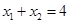 .
.
显然直线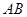 与
与 轴不垂直,设直线
轴不垂直,设直线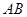 的方程为
的方程为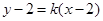 ,即
,即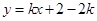 ,将
,将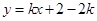 代入
代入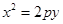 中,
中,
得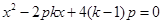 .∴
.∴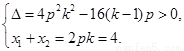
∴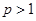 . 故
. 故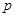 的取值范围为
的取值范围为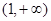 .
.
(II)当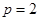 时,由(1)求得
时,由(1)求得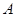 ,
,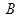 的坐标分别为
的坐标分别为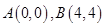 .
.
假设抛物线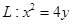 上存在点
上存在点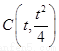 (
(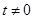 且
且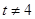 ),使得经过
),使得经过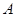 、
、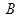 、
、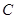 三点的圆和抛物线
三点的圆和抛物线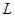 在点
在点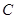 处有相同的切线.
处有相同的切线.
设圆的圆心坐标为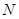
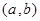 ,
,
∵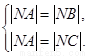 ∴
∴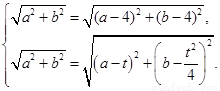
即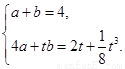 解得
解得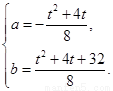
∵抛物线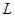 在点
在点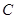 处切线的斜率为
处切线的斜率为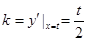 ,而
,而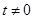 ,且该切线与
,且该切线与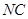 垂直,
垂直,
∴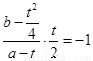 ,即
,即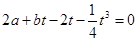 .将
.将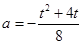 ,
, 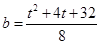
代入上式,得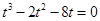 ,即
,即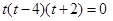 .
.
∵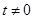 且
且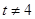 ,∴
,∴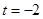 .
.
故满足题设的点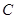 存在,其坐标为
存在,其坐标为 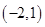 .
.
考点:抛物线的性质运用
点评:解决该试题的关键是利用抛物线的方程以及性质来分析得到结论,同时对于探索性问题,一般先假设,然后分析求解,属于中档题。
