题目内容
5.已知函数f(x)=ax2-lnx+6.(1)若函数f(x)的极值点为x=$\frac{\sqrt{2}}{2}$,求函数f(x)在点(1,f(1))处的切线方程;
(2)当x∈(0,+∞)时,若关于x的不等式f(x)+lnx<x-ln(x+1)+6恒成立,求实数a的取值范围.
分析 (1)先求导,根据f′($\frac{\sqrt{2}}{2}$)=0,求出a的值,再根据导数的几何意义即可求出切线方程,
(2)原不等式转化为ax2<x-ln(x+1),构造函数g(x)=x-ln(x+1),利用导数求出g(x)最小值,继而转化为ax2<0,在x∈((0,+∞)恒成立,求出a的取值范围即可.
解答 解:(1)f(x)=ax2-lnx+6,x>0,
∴f′(x)=2ax-$\frac{1}{x}$,
∵f(x)的极值点为x=$\frac{\sqrt{2}}{2}$,
∴f′($\frac{\sqrt{2}}{2}$)=2a•$\frac{\sqrt{2}}{2}$-$\sqrt{2}$=0,解得a=1,
∴f′(x)=2x-$\frac{1}{x}$,
∴k=f′(1)=2-1=1,f(1)=1-0+6=7,
∴函数f(x)在点(1,f(1))处的切线方程y-7=x-1,即x-y+6=0,
(2)当x∈(0,+∞)时,若关于x的不等式f(x)+lnx<x-ln(x+1)+6恒成立,
∵ax2-lnx+6+lnx<x-ln(x+1)+6在x∈(0,+∞)恒成立,
∴ax2<x-ln(x+1),
设g(x)=x-ln(x+1),
∴g′(x)=1-$\frac{1}{x+1}$>0恒成立,
∴g(x)在x∈(0,+∞)为增函数,
∴g(x)>g(0)=0,
∴ax2<0,在x∈(0,+∞)恒成立,
∴a≤0,
实数a的取值范围为(-∞,0].
点评 本题考查了导数的几何意义和参数的取值范围,关键是转化,构造,求最值,属于中档题.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目
17.已知函数f(x)=x3+bx2+cx+d的图象如图所示,则函数y=log${\;}_{\frac{1}{2}}$(x2+$\frac{2}{3}$bx+$\frac{c}{3}$)的单调减区间为( )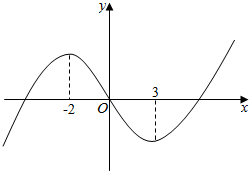

| A. | ($\frac{1}{2}$,+∞) | B. | (3,+∞) | C. | (-∞,-$\frac{1}{2}$) | D. | (-∞,-2) |
 如图,P是正方形ABCD所在平面外一点,PA⊥平面ABCD,AE⊥PD,PA=3AB.求直线AC与平面ABE所成角的正弦值.
如图,P是正方形ABCD所在平面外一点,PA⊥平面ABCD,AE⊥PD,PA=3AB.求直线AC与平面ABE所成角的正弦值.