Question

【题目】已知圆过点，且圆心在直线上.

（1） 求圆的方程；

（2）问是否存在满足以下两个条件的直线:①斜率为；②直线被圆截得的弦为，以为直径的圆过原点. 若存在这样的直线，请求出其方程；若不存在，请说明理由.

Answer 1

【答案】(1) ;(2) 存在这样的两条直线，其方程是或

【解析】

试题(1)将方程设为圆的一般方程，，根据条件表示为的三元一次方程，解方程组即求得圆的方程；

（2）首先设直线存在，其方程为，它与圆C的交点设为A、B

然后联立直线与圆的方程，得到根与系数的关系，根据,得到，代入直线方程与根与系数的关系解得b，得到直线方程，并需验证.

试题解析：解：(Ⅰ)设圆C的方程为

则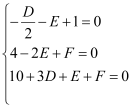 ∴解得 D=-6, E=4, F=4

∴圆C方程为:

即

(Ⅱ)设直线存在，其方程为，它与圆C的交点设为A、B

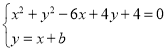则由 得（＊）

∴

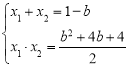
∵AB为直径, ∴ ∴，

∴，

即 ， 即，

∴或

容易验证或时方程（＊）的

故存在这样的两条直线，其方程是或