题目内容
【题目】在平面直角坐标系xOy中,已知圆C:![]() ,直线l:
,直线l:![]() .
.
![]() 当
当![]() 时,若圆C与直线l交于A,B两点,过点A,B分别作l的垂线与y轴交于D,E两点,求
时,若圆C与直线l交于A,B两点,过点A,B分别作l的垂线与y轴交于D,E两点,求![]() 的值;
的值;
![]() 过直线l上的任意一点P作圆的切线
过直线l上的任意一点P作圆的切线![]() 为切点
为切点![]() ,若平面上总存在定点N,使得
,若平面上总存在定点N,使得![]() ,求圆心C的横坐标的取值范围.
,求圆心C的横坐标的取值范围.
【答案】(1)4(2)![]() .
.
【解析】
(1)当a=﹣1时,联立直线与圆的方程求出A,B的坐标,再求出D,E的坐标,就可以算出|DE|;
(2)设出P(m,m+3),N(x0,y0),由PQ=PN得|PQ|2=|PN|2,得|PC|2﹣4=|PN|2,再将此式坐标化,然后先对m恒成立,再对y0有解,可求出a的取值范围.
![]() 时,圆C:
时,圆C:![]() ,
,
与直线l:![]() 的交点
的交点![]() ,
,![]() ,
,
![]() 直线AD:
直线AD:![]() ,直线BE:
,直线BE:![]() ,
,
令![]() ,分别得
,分别得![]() ,
,![]() ,
,
![]() ,
,![]() .
.
![]() ;
;
![]() 设
设![]() ,定点
,定点![]() ,
,
由题意可得,![]() ,
,
![]() ,
,
![]() ,
,
依题意对任意的m,
都有![]()
![]() 成立,
成立,
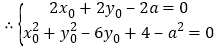 ,消去
,消去![]() 并整理得:
并整理得:![]() 对
对![]() 有解,
有解,
所以![]() ,解得:
,解得:![]() 或
或![]()
故圆心C的横坐标a的取值范围是:![]() .
.

练习册系列答案
相关题目