题目内容
在△ABC中,已知tan =sinC,给出以下四个论断:①tanA•cotB=1,②1<sinA+sinB≤
=sinC,给出以下四个论断:①tanA•cotB=1,②1<sinA+sinB≤ ,③sin2A+cos2B=1,④cos2A+cos2B=sin2C,其中正确的是
,③sin2A+cos2B=1,④cos2A+cos2B=sin2C,其中正确的是
- A.①③
- B.②④
- C.①④
- D.②③
B
分析:先利用同角三角函数的基本关系和二倍角公式化简整理题设等式求得cos =
= 进而求得A+B=90°进而求得①tanA•cotB=tanA•tanA等式不一定成立,排除;②利用两角和公式化简,利用正弦函数的性质求得其范围符合,②正确;
进而求得A+B=90°进而求得①tanA•cotB=tanA•tanA等式不一定成立,排除;②利用两角和公式化简,利用正弦函数的性质求得其范围符合,②正确;
③sin2A+cos2B=2sin2A不一定等于1,排除③;④利用同角三角函数的基本关系可知cos2A+cos2B=cos2A+sin2A=1,进而根据C=90°可知sinC=1,进而可知二者相等.④正确.
解答:∵tan =sinC
=sinC
∴ =2sin
=2sin cos
cos
整理求得cos(A+B)=0
∴A+B=90°.
∴tanA•cotB=tanA•tanA不一定等于1,①不正确.
∴sinA+sinB=sinA+cosA= sin(A+45°)
sin(A+45°)
45°<A+45°<135°,
 <sin(A+45°)≤1,
<sin(A+45°)≤1,
∴1<sinA+sinB≤ ,
,
所以②正确
cos2A+cos2B=cos2A+sin2A=1,
sin2C=sin290°=1,
所以cos2A+cos2B=sin2C.
所以④正确.
sin2A+cos2B=sin2A+sin2A=2sin2A=1不一定成立,故③不正确.
综上知②④正确
故选B.
点评:本题主要考查了三角函数的化简求值.考查了学生综合分析问题和推理的能力,基本的运算能力.
分析:先利用同角三角函数的基本关系和二倍角公式化简整理题设等式求得cos
 =
= 进而求得A+B=90°进而求得①tanA•cotB=tanA•tanA等式不一定成立,排除;②利用两角和公式化简,利用正弦函数的性质求得其范围符合,②正确;
进而求得A+B=90°进而求得①tanA•cotB=tanA•tanA等式不一定成立,排除;②利用两角和公式化简,利用正弦函数的性质求得其范围符合,②正确;③sin2A+cos2B=2sin2A不一定等于1,排除③;④利用同角三角函数的基本关系可知cos2A+cos2B=cos2A+sin2A=1,进而根据C=90°可知sinC=1,进而可知二者相等.④正确.
解答:∵tan
 =sinC
=sinC∴
 =2sin
=2sin cos
cos
整理求得cos(A+B)=0
∴A+B=90°.
∴tanA•cotB=tanA•tanA不一定等于1,①不正确.
∴sinA+sinB=sinA+cosA=
 sin(A+45°)
sin(A+45°)45°<A+45°<135°,
 <sin(A+45°)≤1,
<sin(A+45°)≤1,∴1<sinA+sinB≤
 ,
,所以②正确
cos2A+cos2B=cos2A+sin2A=1,
sin2C=sin290°=1,
所以cos2A+cos2B=sin2C.
所以④正确.
sin2A+cos2B=sin2A+sin2A=2sin2A=1不一定成立,故③不正确.
综上知②④正确
故选B.
点评:本题主要考查了三角函数的化简求值.考查了学生综合分析问题和推理的能力,基本的运算能力.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
 )
) ,H是△ABC的垂心,且
,H是△ABC的垂心,且 .
. 的直线与轨迹M交于点P,点Q(t,0)是x轴上任意一点,求当△CPQ为锐角三角形时t的取值范围.
的直线与轨迹M交于点P,点Q(t,0)是x轴上任意一点,求当△CPQ为锐角三角形时t的取值范围.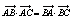 .
. |=|
|=| |;
|; ,求|
,求| -t
-t