题目内容
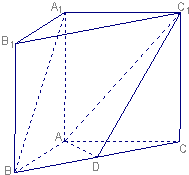 如图,在三棱柱A1B1C1-ABC中,A1A⊥平面ABC,A1A=AB=AC,AB⊥AC,点D是BC上一点,且AD⊥C1D.
如图,在三棱柱A1B1C1-ABC中,A1A⊥平面ABC,A1A=AB=AC,AB⊥AC,点D是BC上一点,且AD⊥C1D.(1)求证:平面ADC1⊥平面BCC1B1;
(2)求证:A1B∥平面ADC1;
(3)求二面角C-AC1-D大小的余弦值.
分析:(1)要证明面面垂直,需要先证明线面垂直,找出AD⊥平面BC1,又AD?平面ABC,根据面面垂直的判断得到结论.
(2)根据有中点连中点的方法,做出辅助线,得到线与线平行,利用线面平行的判定定理得到结论.
(3)建立坐标系,写出要用的点的坐标,设出平面的法向量,求出这个法向量,另一个平面的法向量可以直接写出,根据两个平面的法向量求出面面夹角的余弦值.
(2)根据有中点连中点的方法,做出辅助线,得到线与线平行,利用线面平行的判定定理得到结论.
(3)建立坐标系,写出要用的点的坐标,设出平面的法向量,求出这个法向量,另一个平面的法向量可以直接写出,根据两个平面的法向量求出面面夹角的余弦值.
解答:解: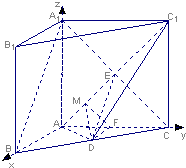 (1)证明:依题意,C1C⊥平面ABC,∵AD?平面ABC∴C1C⊥AD,…(2分)
(1)证明:依题意,C1C⊥平面ABC,∵AD?平面ABC∴C1C⊥AD,…(2分)
又AD⊥C1D,∴C1C∩C1D=C1∴AD⊥平面BC1,又AD?平面ABC…(3分)
∴平面ADC1⊥平面BCC1B1…(4分)
(2)证明:连接A1C交AC1于点E,则E是A1C的中点,连接DE.…(5分)
由(1)知AD⊥平面BC1,∴AD⊥BC,∴D是BC中点…(6分)
∴A1B∥DE…(7分)
又∵DE?平面ADC1,∵A1B?平面ADC1∴A1B∥平面ADC1.…(8分)
(3)如图,建立空间直角坐标系Axyz,设A1A=AB=AC=2,
则A(0,0,0),D(1,1,0),C1(0,2,2).…(9分)
=(1,1,0),
=(0,2,2),
设平面ADC1的一个法向量为
=(x,y,z),
则
•
=0,
•
=0,
即
,令x=1,得y=-1,z=1,
∴
=(1,-1,1).
取平面CAC1的一个法向量为
=(1,0,0),…(11分)
则cos<
,
>=
=
=
.
所以二面角C-AC1-D大小的余弦值为
.…(13分)
 (1)证明:依题意,C1C⊥平面ABC,∵AD?平面ABC∴C1C⊥AD,…(2分)
(1)证明:依题意,C1C⊥平面ABC,∵AD?平面ABC∴C1C⊥AD,…(2分)又AD⊥C1D,∴C1C∩C1D=C1∴AD⊥平面BC1,又AD?平面ABC…(3分)
∴平面ADC1⊥平面BCC1B1…(4分)
(2)证明:连接A1C交AC1于点E,则E是A1C的中点,连接DE.…(5分)
由(1)知AD⊥平面BC1,∴AD⊥BC,∴D是BC中点…(6分)
∴A1B∥DE…(7分)
又∵DE?平面ADC1,∵A1B?平面ADC1∴A1B∥平面ADC1.…(8分)
(3)如图,建立空间直角坐标系Axyz,设A1A=AB=AC=2,
则A(0,0,0),D(1,1,0),C1(0,2,2).…(9分)
| AD |
| AC1 |
设平面ADC1的一个法向量为
| m |
则
| m |
| AD |
| m |
| AC1 |
即
|
∴
| m |
取平面CAC1的一个法向量为
| n |
则cos<
| m |
| n |
| ||||
|
|
| 1 | ||
|
| ||
| 3 |
所以二面角C-AC1-D大小的余弦值为
| ||
| 3 |
点评:本题考查空间向量求二面角及直线与平面的位置关系的证明,第一与第二两个小题主要应用线面关系的判断和性质定理,第三小题解题的关键是建立坐标系,把难度比较大的二面角的求法,转化成了数字的运算,降低了题目难度.

练习册系列答案
相关题目
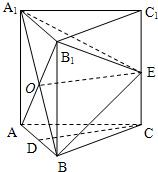 如图,在三棱柱ABC-A1B1C1中,每个侧面均是边长为2的正方形,D为底边AB的中点,E为侧棱CC1的中点,AB1与A1B的交点为O.
如图,在三棱柱ABC-A1B1C1中,每个侧面均是边长为2的正方形,D为底边AB的中点,E为侧棱CC1的中点,AB1与A1B的交点为O. 16、如图,在三棱柱ABC-A1B1C1中,侧面ABB1A1,ACC1A1均为正方形,∠BAC=90°,D为BC中点.
16、如图,在三棱柱ABC-A1B1C1中,侧面ABB1A1,ACC1A1均为正方形,∠BAC=90°,D为BC中点.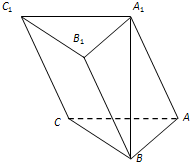 如图,在三棱柱ABC-A1B1C1中,AB⊥AC,顶点在A1底面ABC上的射影恰为点B,且AB=AC=A1B=2.
如图,在三棱柱ABC-A1B1C1中,AB⊥AC,顶点在A1底面ABC上的射影恰为点B,且AB=AC=A1B=2.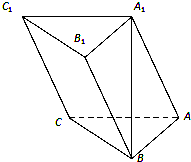 如图,在三棱柱ABC=A1B1C1中,A1B⊥平面ABC,AB⊥AC,且AB=AC=A1B=2.
如图,在三棱柱ABC=A1B1C1中,A1B⊥平面ABC,AB⊥AC,且AB=AC=A1B=2.