题目内容

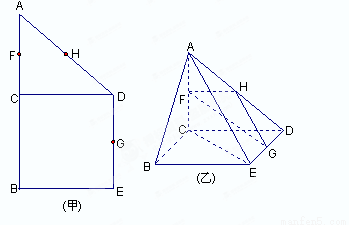
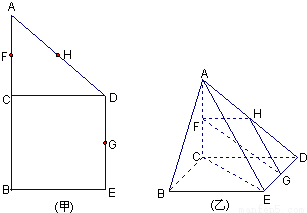
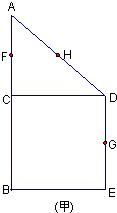 如图(甲),在直角梯形ABED中,AB∥DE,AB⊥BE,AB⊥CD,且BC=CD,AB=2,F、H、G分别为AC,AD,DE的中点,现将△ACD沿CD折起,使平面ACD⊥平面CBED,如图(乙).
如图(甲),在直角梯形ABED中,AB∥DE,AB⊥BE,AB⊥CD,且BC=CD,AB=2,F、H、G分别为AC,AD,DE的中点,现将△ACD沿CD折起,使平面ACD⊥平面CBED,如图(乙).(1)求证:平面FHG∥平面ABE;
(2)记BC=xV(x)表示三棱锥B-ACE的体积,求V(x)的最大值.
分析:(1)欲证平面FHG∥平面ABE,根据面面平行的判定定理可知只需在一个平面内找两相交直线与另一平面平行,由图(甲)结合已知条件知四边形CBED为正方形,根据线面平行的判定定理可知FH∥面ABE,同理可得HG∥面ABE又FH∩HG=H满足定理所需条件;
(2)根据面面垂直的性质可知AC⊥平面CBED,从而V(x)=VA-BCE=
S△BCE•AC=
×
x2(2-x)=
x2(2-x),然后利用导数法求出体积的最大值即可.
(2)根据面面垂直的性质可知AC⊥平面CBED,从而V(x)=VA-BCE=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 6 |
解答:解:(1)证明:由图(甲)结合已知条件知四边形CBED为正方形
如图(乙)∵F、H、G分别为AC,AD,DE的中点
∴FH∥CD,HG∥AE(1分)
∵CD∥BE∴FH∥BE
∵BE?面ABE,FH?面ABE
∴FH∥面ABE(3分)
同理可得HG∥面ABE又∵FH∩HG=H∴平面FHG∥平面ABE(4分)
(2)∵平面ACD⊥平面CBED且AC⊥CD
∴AC⊥平面CBED(5分)
∴V(x)=VA-BCE=
S△BCE•AC=H
∵BC=x∴AC=2-X(0<x<2)
∴V(x)=
×
x2(2-x)=
x2(2-x)=
x•x•(4-2x)(7分)
∵V′(x)=
(4x-3x2),令V′(x)=0得x=0(不合舍去)或x=
当x>
时V′(x)<0,当0<x<
时V′(x)>0
∴当x=
时V(x)有最大值,V(x)max=V(
)=
如图(乙)∵F、H、G分别为AC,AD,DE的中点
∴FH∥CD,HG∥AE(1分)
∵CD∥BE∴FH∥BE
∵BE?面ABE,FH?面ABE
∴FH∥面ABE(3分)
同理可得HG∥面ABE又∵FH∩HG=H∴平面FHG∥平面ABE(4分)
(2)∵平面ACD⊥平面CBED且AC⊥CD
∴AC⊥平面CBED(5分)
∴V(x)=VA-BCE=
| 1 |
| 3 |
∵BC=x∴AC=2-X(0<x<2)
∴V(x)=
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 6 |
| 1 |
| 12 |
∵V′(x)=
| 1 |
| 6 |
| 4 |
| 3 |
当x>
| 4 |
| 3 |
| 4 |
| 3 |
∴当x=
| 4 |
| 3 |
| 4 |
| 3 |
| 16 |
| 81 |
点评:本题考查平面与平面垂直的判定,三棱锥的体积最值的计算,体积的求解在最近两年高考中频繁出现,值得重视.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
 如图(甲),在直角梯形ABED中,AB∥DE,AB⊥BE,AB⊥CD,且BC=CD,AB=2,F、H、G分别为AC,AD,DE的中点,现将△ACD沿CD折起,使平面ACD⊥平面CBED,如图(乙).
如图(甲),在直角梯形ABED中,AB∥DE,AB⊥BE,AB⊥CD,且BC=CD,AB=2,F、H、G分别为AC,AD,DE的中点,现将△ACD沿CD折起,使平面ACD⊥平面CBED,如图(乙). BE,AB
BE,AB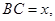
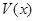 表示三棱锥B-ACE
的体积,求
表示三棱锥B-ACE
的体积,求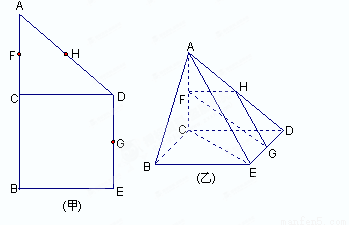
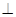 BE,AB
BE,AB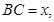
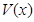 表示三棱锥B-ACE
的体积,求
表示三棱锥B-ACE
的体积,求