题目内容
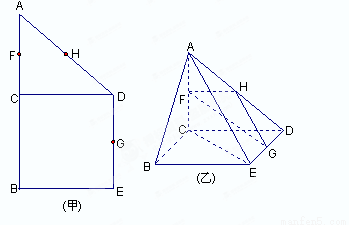
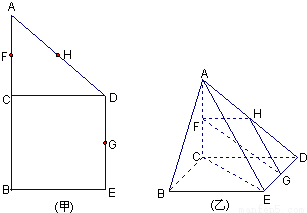
 如图(甲),在直角梯形ABED中,AB∥DE,AB⊥BE,AB⊥CD,且BC=CD,AB=2,F、H、G分别为AC,AD,DE的中点,现将△ACD沿CD折起,使平面ACD⊥平面CBED,如图(乙).
如图(甲),在直角梯形ABED中,AB∥DE,AB⊥BE,AB⊥CD,且BC=CD,AB=2,F、H、G分别为AC,AD,DE的中点,现将△ACD沿CD折起,使平面ACD⊥平面CBED,如图(乙).(1)求证:平面FHG∥平面ABE;
(2)记BC=x,V(x)表示三棱锥B-ACE的体积,求V(x)的最大值;
(3)当V(x)取得最大值时,求二面角D-AB-C的余弦值.Pn(xn,yn)
分析:(1)欲证平面FHG∥平面ABE,只需证明线面平行,故只需要在平面FHG中寻找两条相交直线与平面平行;
(2)由于平面ACD⊥平面CBED 且AC⊥CD,所以AC⊥平面CBED,故可表示三棱锥B-ACE的体积,利用基本不等式求最值,注意等号成立的条件;
(3)求解二面角D-AB-C的余弦值,建立空间直角坐标系,利用向量法求解,分别求出平面ACB的法向量,平面ABD的法向量,利用cosθ=
可以求解
(2)由于平面ACD⊥平面CBED 且AC⊥CD,所以AC⊥平面CBED,故可表示三棱锥B-ACE的体积,利用基本不等式求最值,注意等号成立的条件;
(3)求解二面角D-AB-C的余弦值,建立空间直角坐标系,利用向量法求解,分别求出平面ACB的法向量,平面ABD的法向量,利用cosθ=
| ||||
|
|
解答:解: (1)证明:由图(甲)结合已知条件知四边形CBED为正方形
(1)证明:由图(甲)结合已知条件知四边形CBED为正方形
如图(乙)∵F、H、G分别为AC,AD,DE的中点
∴FH∥CD,HG∥AE--------------------------------------(1分)
∵CD∥BE∴FH∥BE
∵BE?面ABE,FH?面ABE
∴FH∥面ABE-------------------------------------(3分)
同理可得HG∥面ABE
又∵FH∩HG=H
∴平面FHG∥平面ABE-----------------(4分)
(2)∵平面ACD⊥平面CBED 且AC⊥CD
∴AC⊥平面CBED----------------------------------------------------(5分)
∴V(x)=VA-BCE=
S△BCE•AC
∵BC=x∴AC=2-x(0<x<2)
∴V(x)=
×
x2(2-x)=
x2(2-x)=
x•x•(4-2x)--------------(7分)
∵x•x•(4-2x)≤(
)3=
∴V(x)≤
×
=
当且仅当x=4-2x即x=
时取“=”
∴V(x)的最大值为
-------------------------------------------(9分)
(3)以点C为坐标原点,CB为x轴建立空间直角坐标系
如右图示:由(2)知当V(x)取得最大值时x=
,即BC=
这时AC=
,∴B(
,0,0),D(0,
,0),A(0,0,
)-----(10分)
∴平面ACB的法向量
=(0,
,0)
设平面ABD的法向量为
=(a,b,c)
∵
=(
,0,-
),
=(-
,
,0)-------------(11分)
由
⊥
,
⊥
得-
a+
b=0,
a-
c=0
令c=1得
=(
,
,1)----------------------------------------(12分)
设二面角D-AB-C为θ,则cosθ=
=
=
---(14分)
 (1)证明:由图(甲)结合已知条件知四边形CBED为正方形
(1)证明:由图(甲)结合已知条件知四边形CBED为正方形如图(乙)∵F、H、G分别为AC,AD,DE的中点
∴FH∥CD,HG∥AE--------------------------------------(1分)
∵CD∥BE∴FH∥BE
∵BE?面ABE,FH?面ABE
∴FH∥面ABE-------------------------------------(3分)
同理可得HG∥面ABE
又∵FH∩HG=H
∴平面FHG∥平面ABE-----------------(4分)
(2)∵平面ACD⊥平面CBED 且AC⊥CD
∴AC⊥平面CBED----------------------------------------------------(5分)
∴V(x)=VA-BCE=
| 1 |
| 3 |
∵BC=x∴AC=2-x(0<x<2)
∴V(x)=
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 6 |
| 1 |
| 12 |
∵x•x•(4-2x)≤(
| x+x+4-2x |
| 3 |
| 64 |
| 27 |
∴V(x)≤
| 1 |
| 12 |
| 64 |
| 27 |
| 16 |
| 81 |
当且仅当x=4-2x即x=
| 4 |
| 3 |
∴V(x)的最大值为
| 16 |
| 81 |
(3)以点C为坐标原点,CB为x轴建立空间直角坐标系
如右图示:由(2)知当V(x)取得最大值时x=
| 4 |
| 3 |
| 4 |
| 3 |
这时AC=
| 2 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 2 |
| 3 |

∴平面ACB的法向量
| CD |
| 4 |
| 3 |
设平面ABD的法向量为
| m |
∵
| AB |
| 4 |
| 3 |
| 2 |
| 3 |
| BD |
| 4 |
| 3 |
| 4 |
| 3 |
由
| m |
| AB |
| m |
| BD |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 2 |
| 3 |
令c=1得
| m |
| 1 |
| 2 |
| 1 |
| 2 |
设二面角D-AB-C为θ,则cosθ=
| ||||
|
|
| ||||||||
|
| ||
| 6 |
点评:本题的考点是面面平行的判断,主要考查证明面面平行,考查几何体的体积,考查二面角的平面角,关键是正确运用面面平行的判定,利用向量法求面面角,关键是求出相应的法向量.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目

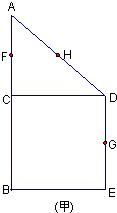 如图(甲),在直角梯形ABED中,AB∥DE,AB⊥BE,AB⊥CD,且BC=CD,AB=2,F、H、G分别为AC,AD,DE的中点,现将△ACD沿CD折起,使平面ACD⊥平面CBED,如图(乙).
如图(甲),在直角梯形ABED中,AB∥DE,AB⊥BE,AB⊥CD,且BC=CD,AB=2,F、H、G分别为AC,AD,DE的中点,现将△ACD沿CD折起,使平面ACD⊥平面CBED,如图(乙). BE,AB
BE,AB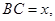
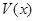 表示三棱锥B-ACE
的体积,求
表示三棱锥B-ACE
的体积,求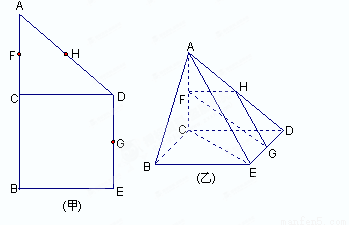
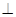 BE,AB
BE,AB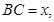
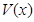 表示三棱锥B-ACE
的体积,求
表示三棱锥B-ACE
的体积,求