题目内容
已知函数y=xlnx，则其在点x=1处的切线方程是（ ）A．y=2x-2
B．y=2x+2
C．y=x-1
D．y=x+1
【答案】分析：运用求导公式计算x=1时的斜率，再结合曲线上一点求出切线方程．
解答：解：y=xlnx y'=1×lnx+x•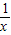
=1+lnx y'（1）=1 又当x=1时y=0∴切线方程为y=x-1 故选C．
点评：此题主要考查导数的计算，比较简单．
解答：解：y=xlnx y'=1×lnx+x•
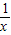=1+lnx y'（1）=1 又当x=1时y=0∴切线方程为y=x-1 故选C．点评：此题主要考查导数的计算，比较简单．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
已知函数y=xlnx，则其在点x=1处的切线方程是（ ）
| A、y=2x-2 | B、y=2x+2 | C、y=x-1 | D、y=x+1 |
已知函数y=xlnx，则其在点x=e处的切线方程是（ ）
| A、y=2x-e | B、y=e | C、y=x-e | D、y=x+e |