题目内容
已知点P为锐二面角α-l-β内的一点，点P到平面α，β及棱l的距离之比为1：
：
，则此二面角的大小是______．
| ||
| 2 |
| 2 |
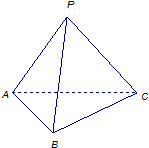
过P点向平面α平面β和直线l做垂线，垂足分别为A，B，0，连接AO，BO，如下图所示：
则AO⊥l，bO⊥l，∠AOB锐二面角α-l-β的平面角，
又∵PA：PB：PO=1：
：
，
∴∠AOP=45°，∠BOP=30°
∴∠AOB=75°
故答案为：75°
则AO⊥l，bO⊥l，∠AOB锐二面角α-l-β的平面角，
又∵PA：PB：PO=1：
| ||
| 2 |
| 2 |
∴∠AOP=45°，∠BOP=30°
∴∠AOB=75°
故答案为：75°
练习册系列答案
学而优衔接教材南京大学出版社系列答案
小学课堂作业系列答案
相关题目
已知边长为
α,PQ与l成45°角,与β成30°角,则二面角α-l-β的大小为___________.
，则此二面角的大小是（ ）。