题目内容
已知离心率为e=2的双曲线C:(Ⅰ)求双曲线C的方程;
(Ⅱ)过点M(5,0)的直线l与双曲线C交于A、B两点,若![]() ,求直线l的方程.
,求直线l的方程.
解:(Ⅰ)∵e=2,∴![]() =2①
=2①
设右焦点F(c,0)关于直线x+y+![]() =0的对称点为(x0,y0)
=0的对称点为(x0,y0)
则 解得x0=
解得x0=![]() ,∴
,∴![]() ②
②
由①②得![]() ,从而b=
,从而b=![]() ,∴双曲线方程是x2-
,∴双曲线方程是x2-![]() =1
=1
(Ⅱ)设直线l:y=k(x-5),A(x1,y1),B(x2,y2)
∵![]() ,∴(x2-x1,y2-y1)=3(5-x2,-y2)
,∴(x2-x1,y2-y1)=3(5-x2,-y2)
∴x2-x1=3(5-x2),x1=4x2-15①
由 ,得(3-k2)x2+10k2x-25k2-3=0
,得(3-k2)x2+10k2x-25k2-3=0
 ②
②
x1+x2=![]() ③ x1·x2=
③ x1·x2=![]() ④
④
由①②得 代入④得
代入④得![]()
解得k=±1满足②
∴l方程为x-y-5=0或x+y-5=0 。

练习册系列答案
相关题目
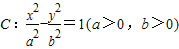 ,双曲线C的一个焦点到渐近线的距离是
,双曲线C的一个焦点到渐近线的距离是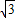
 ,且
,且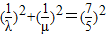 时,求直线l的方程.
时,求直线l的方程.