题目内容
已知离心率为e=2的双曲线C：
-
=1(a＞0，b＞0)，双曲线C的一个焦点到渐近线的距离是
（1）求双曲线C的方程
（2）过点M（5，0）的直线l与双曲线C交于A、B两点，交y轴于N点，当
=λ
=μ
，且(
)2+(
)2=(
)2时，求直线l的方程．
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
（1）求双曲线C的方程
（2）过点M（5，0）的直线l与双曲线C交于A、B两点，交y轴于N点，当
| NM |
| AM |
| BM |
| 1 |
| λ |
| 1 |
| μ |
| 7 |
| 5 |
（1）∵e=2∴
=2（1分）
右焦点F（c，0）到渐近线bx-ay=0的距离d=
=b=
（3分）
从而得a=1∴双曲线方程是x2-
=1（5分）
（2）设A（x1，y1），B（x2，y2）
由
得（3-k2）x2+10k2x-25k2-3=0△=100k4+4(3-k2)(25k2+3)＞0(k≠±
)①x1+x2=-
，x1x2=-
由
=λ
得，同理
=1-
+
=2-
=
，
•
=1-
+
=
(
)2+(
)2=(
+
)2-
=
-
=
解得k=±3满足①∴l方程为3x-y-15=0或3x+y-15=0
| c |
| a |
右焦点F（c，0）到渐近线bx-ay=0的距离d=
| |cb| | ||
|
| 3 |
从而得a=1∴双曲线方程是x2-
| y2 |
| 3 |
（2）设A（x1，y1），B（x2，y2）
由
|
| 3 |
| 10k2 |
| 3-k2 |
| 25k2+3 |
| 3-k2 |
由
| NM |
| AM |
| 1 |
| μ |
| x2 |
| 5 |
| 1 |
| λ |
| 1 |
| μ |
| x1+x2 |
| 5 |
| 6 |
| 3-k2 |
| 1 |
| λ |
| 1 |
| μ |
| x1+x2 |
| 5 |
| x1x2 |
| 25 |
| 72 |
| 25(3-k2) |
| 1 |
| λ |
| 1 |
| μ |
| 1 |
| λ |
| 1 |
| μ |
| 2 |
| λμ |
| 36 |
| (3-k2)2 |
| 144 |
| 25(3-k2) |
| 49 |
| 25 |
解得k=±3满足①∴l方程为3x-y-15=0或3x+y-15=0
练习册系列答案
智慧小复习系列答案
相关题目
-=1(a＞0，b＞0)，双曲线C的右焦点关于直线x+y+
=0的对称点在双曲线C的左准线上.
，且
=3时，求直线l的方程.
=1(a＞0，b＞0)，双曲线C的右焦点关于直线x+y+
=0的对称点在双曲线C的左准线上．
，求直线l的方程．
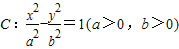，双曲线C的一个焦点到渐近线的距离是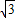
，且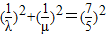
时，求直线l的方程．