题目内容
已知三点A,B,C满足AB=3,BC=4,CA=5,则
•
+
•
+
•
=
| AB |
| BC |
| BC |
| CA |
| CA |
| AB |
-25
-25
.分析:由题意可得,AB⊥BC,
•
=0,再利用两个向量的数量积的定义以及直角三角形中的边角关系,求得要求式子的值.
| AB |
| BC |
解答:解:由题意可得,AB⊥BC,∴
•
=0.
故
•
+
•
+
•
=0+4×5×cos(π-C)+5×3×cos(π-A)
=-20cosC-15cosA=-20×
-15×
=-25,
故答案为-25.
| AB |
| BC |
故
| AB |
| BC |
| BC |
| CA |
| CA |
| AB |
=-20cosC-15cosA=-20×
| 4 |
| 5 |
| 3 |
| 5 |
故答案为-25.
点评:本题主要考查两个向量的数量积的定义,直角三角形中的边角关系,注意两个向量的夹角,属于中档题.

练习册系列答案
相关题目
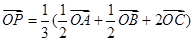 ,则点 P 一定为三角形的 ( )
,则点 P 一定为三角形的 ( )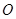 是平面上的一定点,
是平面上的一定点,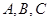 是平面上不共线的三点,动点
是平面上不共线的三点,动点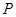 满
满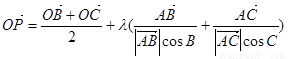 ,
, ,则动点
,则动点 的( ).
的( ).