题目内容
已知命题p:?x∈(-∞,0),2x<3x;命题q: ,则下列命题为真命题的是
,则下列命题为真命题的是
- A.p∧q
- B.p∨(﹁q)
- C.(﹁p)∧q
- D.p∧(﹁q)
C
分析:由指数函数y=2x与y=3x的图象易知x∈(-∞,0)时,2x>3x,则p是假命题;由余弦函数y=cosx的值域易知x∈(0, )时,0<cosx<1,则q是真命题,然后根据复合命题的真假关系即可作出判断.
)时,0<cosx<1,则q是真命题,然后根据复合命题的真假关系即可作出判断.
解答: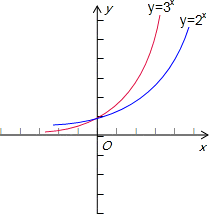 解:由指数函数y=2x与y=3x的图象可知:?x∈(-∞,0),2x>3x,
解:由指数函数y=2x与y=3x的图象可知:?x∈(-∞,0),2x>3x,
∴命题p是假命题;
∵x∈(0, ),0<cosx<1∴命题q是真命题.
),0<cosx<1∴命题q是真命题.
可见:p∧q是假命题,p∨(﹁q)是假命题,(﹁p)∧q是真命题,p∧(﹁q)是假命题.
故选C.
点评:本题主要考查复合命题的真假关系,同时考查指数函数的图象与余弦函数的值域.
分析:由指数函数y=2x与y=3x的图象易知x∈(-∞,0)时,2x>3x,则p是假命题;由余弦函数y=cosx的值域易知x∈(0,
 )时,0<cosx<1,则q是真命题,然后根据复合命题的真假关系即可作出判断.
)时,0<cosx<1,则q是真命题,然后根据复合命题的真假关系即可作出判断.解答:
 解:由指数函数y=2x与y=3x的图象可知:?x∈(-∞,0),2x>3x,
解:由指数函数y=2x与y=3x的图象可知:?x∈(-∞,0),2x>3x,∴命题p是假命题;
∵x∈(0,
 ),0<cosx<1∴命题q是真命题.
),0<cosx<1∴命题q是真命题.可见:p∧q是假命题,p∨(﹁q)是假命题,(﹁p)∧q是真命题,p∧(﹁q)是假命题.
故选C.
点评:本题主要考查复合命题的真假关系,同时考查指数函数的图象与余弦函数的值域.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
已知命题p:?x∈R,2x2+2x+
<0;命题q:?x∈R,sinx-cosx=
.则下列判断正确的是( )
| 1 |
| 2 |
| 2 |
| A、p是真命题 |
| B、q是假命题 |
| C、¬P是假命题 |
| D、¬q是假命题 |