题目内容
(本小题满分12分)已知函数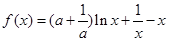 (
(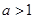 ).
).
(1)试讨论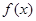 在区间
在区间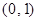 上的单调性;
上的单调性;
(2)当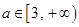 时,曲线
时,曲线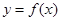 上总存在相异两点
上总存在相异两点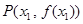 ,
,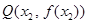 ,使得曲线
,使得曲线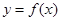 在点
在点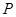 ,
,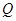 处的切线互相平行,求证:
处的切线互相平行,求证: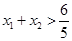 .
.
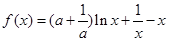 (
(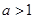 ).
).(1)试讨论
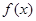 在区间
在区间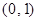 上的单调性;
上的单调性;(2)当
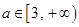 时,曲线
时,曲线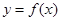 上总存在相异两点
上总存在相异两点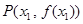 ,
,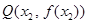 ,使得曲线
,使得曲线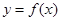 在点
在点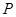 ,
,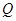 处的切线互相平行,求证:
处的切线互相平行,求证: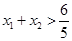 .
. (1)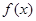 在
在 上单调递减,在
上单调递减,在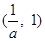 上单调递增. (2)证明:见解析。
上单调递增. (2)证明:见解析。
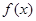 在
在 上单调递减,在
上单调递减,在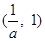 上单调递增. (2)证明:见解析。
上单调递增. (2)证明:见解析。本试题主要是考查了导数在研究函数的运用。
(1)由已知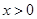 ,
,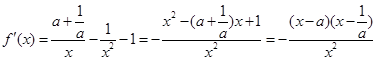 ,根据导数的符号判定函数单调性,得到结论。
,根据导数的符号判定函数单调性,得到结论。
(2)因为由题意可得,当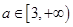 时,
时,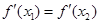 (
(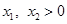 ,且
,且 ).
).
即 ,
,
所以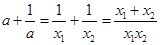 ,
,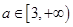 .,借助于不等式来证明。
.,借助于不等式来证明。
(1)由已知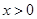 ,
,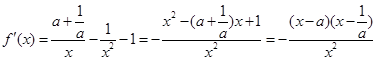 .
.
由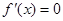 ,得
,得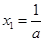 ,
,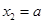 . 因为
. 因为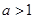 ,所以
,所以 ,且
,且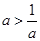 .
.
所以在区间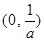 上,
上, ;在区间
;在区间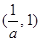 上,
上,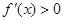 .
.
故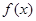 在
在 上单调递减,在
上单调递减,在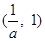 上单调递增. ……………6分
上单调递增. ……………6分
(2)证明:由题意可得,当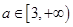 时,
时,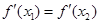 (
(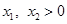 ,且
,且 ).
).
即 ,
,
所以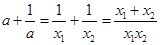 ,
,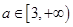 . ………8分
. ………8分
因为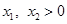 ,且
,且 ,所以
,所以 恒成立,
恒成立,
所以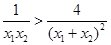 ,又
,又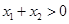 ,
,
所以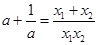
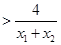 ,整理得
,整理得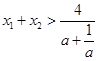 .
.
令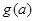
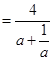 ,因为
,因为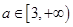 ,所以
,所以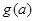 在
在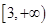 上单调递减,
上单调递减,
所以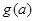
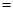
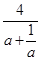 在
在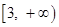 上的最大值为
上的最大值为 , 所以
, 所以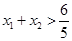 .…………12分
.…………12分
(1)由已知
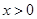 ,
,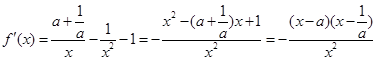 ,根据导数的符号判定函数单调性,得到结论。
,根据导数的符号判定函数单调性,得到结论。(2)因为由题意可得,当
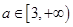 时,
时,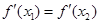 (
(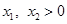 ,且
,且 ).
).即
 ,
,所以
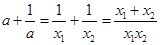 ,
,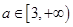 .,借助于不等式来证明。
.,借助于不等式来证明。(1)由已知
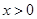 ,
,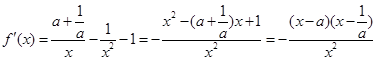 .
. 由
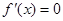 ,得
,得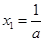 ,
,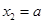 . 因为
. 因为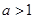 ,所以
,所以 ,且
,且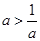 .
.所以在区间
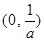 上,
上, ;在区间
;在区间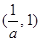 上,
上,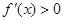 .
.故
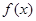 在
在 上单调递减,在
上单调递减,在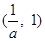 上单调递增. ……………6分
上单调递增. ……………6分(2)证明:由题意可得,当
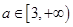 时,
时,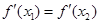 (
(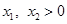 ,且
,且 ).
).即
 ,
,所以
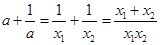 ,
,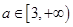 . ………8分
. ………8分因为
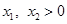 ,且
,且 ,所以
,所以 恒成立,
恒成立,所以
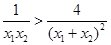 ,又
,又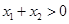 ,
,所以
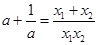
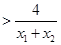 ,整理得
,整理得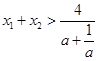 .
. 令
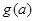
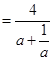 ,因为
,因为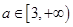 ,所以
,所以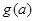 在
在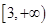 上单调递减,
上单调递减,所以
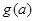
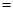
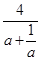 在
在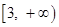 上的最大值为
上的最大值为 , 所以
, 所以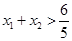 .…………12分
.…………12分
练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
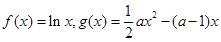 ,(
,(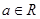 ).
).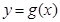 的零点至少有一个在原点右侧,求实数
的零点至少有一个在原点右侧,求实数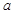 的范围.
的范围.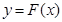 的图象为曲线
的图象为曲线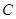 .设点
.设点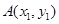 ,
,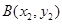 是曲线
是曲线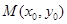 ,使得:①
,使得:①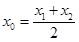 ;②曲线
;②曲线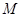 处的切线平行于直线
处的切线平行于直线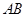 ,则称函数
,则称函数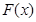 存在“中值相依切线”.
存在“中值相依切线”. (
(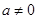 )是否存在“中值相依切线”,请说明理由.
)是否存在“中值相依切线”,请说明理由. 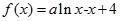 ,(
,(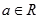 ),曲线
),曲线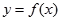 在点
在点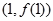 处的切线垂直于
处的切线垂直于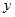 轴.
轴.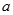 的值;
的值;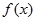 的极值.
的极值.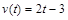 (
(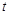 的单位:秒,
的单位:秒,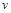 的单位:米/秒)的速度做变速直线运动,则该物体从时刻
的单位:米/秒)的速度做变速直线运动,则该物体从时刻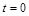 到5秒运动的路程
到5秒运动的路程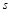 为 米.
为 米.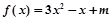 ,
,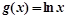 ,若函数
,若函数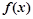 与
与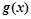 的图象在
的图象在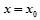 处的切线平行,则
处的切线平行,则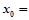 .
. 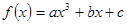 在点
在点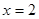 处取得极值
处取得极值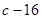 。
。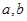 的值;
的值;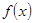 有极大值28,求
有极大值28,求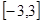 上的最小值。
上的最小值。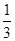
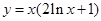 在点(1,1)处的切线方程是____________________
在点(1,1)处的切线方程是____________________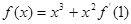 在点
在点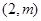 处的切线斜率为 .
处的切线斜率为 .