题目内容
求证:
证法一:令t=tan![]() ,则左边=
,则左边=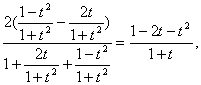
右边=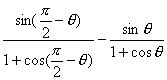
=tan(![]() -
-![]() )-tan
)-tan![]()
=![]() .
.
左边=右边,即得证.
证法二:要证![]()
∵![]()
=![]()
=![]()
∴只要证![]() ,
,
若cosθ-sinθ=0,则等式显然成立.
∴只要证![]() ,
,
即证(1+sinθ+cosθ)2=2(1+sinθ)(1+cosθ).
∵(1+sinθ+cosθ)2=1+sin2θ+cos2θ+2sinθ+2cosθ+2sinθ·cosθ=2(1+sinθ+cosθ+sinθ·cosθ),
又2(1+sinθ)(1+cosθ)=2(1+sinθ+cosθ+sinθcosθ),
∴上式成立,即得证原等式成立.

练习册系列答案
相关题目