题目内容
(本小题满分12分)
有编号为l,2,3,…, 的
的 个学生,入坐编号为1,2,3,…,
个学生,入坐编号为1,2,3,…, 的
的 个座位.每个学生规定坐一个座位,设学生所坐的座位号与该生的编号不同的学生人数为
个座位.每个学生规定坐一个座位,设学生所坐的座位号与该生的编号不同的学生人数为 ,已知
,已知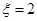 时,共有6种坐法.
时,共有6种坐法.
(1)求 的值;
的值;
(2)求随机变量 的概率分布列和数学期望.
的概率分布列和数学期望.
(1) ……………10分 (2)
(2)
0 2 3
4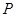





解析试题分析:解:(1)当 ……………10分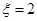 时,有
时,有 种坐法,
种坐法, ,即
,即 , ……………2分
, ……………2分 或
或 舍去.
舍去.  ……………4分
……………4分
(2) 的可能取值是0,2,3,4
的可能取值是0,2,3,4
又
 ……………8分
……………8分 的概率分布列为
的概率分布列为
则
0 2 3
4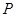




 . ……………12分
. ……………12分
考点:随机变量 的概率分布列;数学期望。
的概率分布列;数学期望。
点评:本题属基础题。但在本题中,需要注意随机变量 不能取1。
不能取1。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
(8分)对某校高一年级学生参加社区服务次数进行统计,随机抽取 名学生作为样本,得到这
名学生作为样本,得到这 名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下:
名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下:
| 分组 | 频数 | 频率 |
 | 10 | 0.25 |
 | 25 |  |
 |  |  |
 | 2 | 0.05 |
| 合计 | M | 1 |

⑴求出表中
 、
、 及图中
及图中 的值;
的值;⑵若该校高一学生有720人,试估计他们参加社区服务的次数在区间
 内的人数;
内的人数;⑶在所取样本中,从参加社区服务的次数不少于20次的学生中任选2人,求至多一人参加社区服务次数在区间
 内的概率.
内的概率. 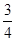 ,甲、丙二人都回答错的概率是
,甲、丙二人都回答错的概率是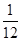 ,乙、丙二人都回答对的概率是
,乙、丙二人都回答对的概率是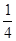 .
.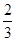 ,服用B有效的概率为
,服用B有效的概率为 。
。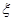 表示这3个试验组中甲类组的个数,求
表示这3个试验组中甲类组的个数,求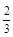 ,且每题正确完成与否互不影响。
,且每题正确完成与否互不影响。 ,参加第五项不合格的概率为
,参加第五项不合格的概率为 。
。  ,求
,求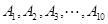 等10所高校举行的自主招生考试,某同学参加每所高校的考试获得通过的概率均为
等10所高校举行的自主招生考试,某同学参加每所高校的考试获得通过的概率均为 .
. 元,该同学决定按
元,该同学决定按 的分布列及数学期望.
的分布列及数学期望.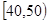 ,
,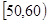 …
…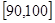 后画出如下部分频率分布直方图,观察图形的信息,回答下列问题:
后画出如下部分频率分布直方图,观察图形的信息,回答下列问题: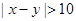 ”的概率.
”的概率.