题目内容
（09年淄博一模）（12分）
如图，已知里棱锥
的底面为直角梯形，
（1）证明平面
平面ABCD；
（2）如果
，且侧面
的面积为8，求四棱锥的面积。
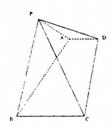
解析：（Ⅰ）取AB、CD 的中点E、F。连结PE、EF、PF，由PA=PB、PC=PD
得
EF为直角梯形的中位线，
又
平面
平面,得
又
且梯形两腰AB、CD必交
（Ⅱ）方法一：由（Ⅰ）及二面角的定义知，
为二面角P-CD-A的平面角等于600
作
于
，连
故
为二面角P-BC-A的平面角
由已知，得
于是
即二面角P-BC-A等于600
方法二：作
，由于PE、EF、EG两两垂直，建立如图所示的空间直角坐标系
由（Ⅰ）及二面角的定义知为二面角的平面角等于600
设平面PBC的法向量为
又平面ABCD的法向量为
二面角P-BC-A的大小为600
练习册系列答案
阅读快车系列答案
相关题目
中，
，一曲线E过点C，动点P在曲线E上运动，并保持
的值不变，直线l经过点A与曲线E交于
两点。
为钝角，求k的取值范围。
，视力在4.6到5.0之间的学生数b，则
的值分别为