题目内容
10.甲、乙两盒中各装有大小相同的小球9个,其中甲盒中红色、黑色、白色小球的个数分别为2,3,4;乙盒中红色、黑色、白色小球的个数均为3.学生A从甲盒中取球,学习B从乙盒中取球.(Ⅰ)若A,B各取一球,求两人所取的球颜色不同的概率;
(Ⅱ)若每人依次各取2球,称同一人手中两球盐酸相同的取法为成功取法,记成功取法次数为X,求X的分布列和数学期望.
分析 (Ⅰ)利用对立事件概率计算公式能求出A,B各取一球,两人所取的球颜色不同的概率.
(Ⅱ)由题意知X的可能取值为0,1,2,分别求出相应的概率,由此能求出X的分布列和EX.
解答 解:(Ⅰ)∵甲、乙两盒中各装有大小相同的小球9个,
其中甲盒中红色、黑色、白色小球的个数分别为2,3,4;
乙盒中红色、黑色、白色小球的个数均为3.学生A从甲盒中取球,学习B从乙盒中取球.
∴A,B各取一球,两人所取的球颜色不同的概率:
P=1-($\frac{2}{9}×\frac{3}{9}+\frac{3}{9}×\frac{3}{9}+\frac{4}{9}×\frac{3}{9}$)=$\frac{2}{3}$.
(Ⅱ)由题意知X的可能取值为0,1,2,
A取球成功的概率P1=$\frac{{C}_{2}^{2}+{C}_{3}^{2}+{C}_{4}^{2}}{{C}_{9}^{2}}$=$\frac{5}{18}$,
B取球成功的概率P2=$\frac{{C}_{3}^{2}+{C}_{3}^{2}+{C}_{3}^{2}}{{C}_{9}^{2}}$=$\frac{1}{4}$,
P(X=0)=(1-$\frac{5}{18}$)(1-$\frac{1}{4}$)=$\frac{13}{24}$,
P(X=1)=(1-$\frac{5}{18}$)×$\frac{1}{4}$+$\frac{5}{18}(1-\frac{1}{4})$=$\frac{7}{18}$,
P(X=2)=$\frac{5}{18}×\frac{1}{4}$=$\frac{5}{72}$,
∴X的分布列为:
| X | 0 | 1 | 2 |
| P | $\frac{13}{24}$ | $\frac{7}{18}$ | $\frac{5}{72}$ |
点评 本题考查概率的求法,考查离散型随机变量的分布列及数学期望的求法,是中档题,解题时要认真审题,注意排列组合知识的合理运用.

 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案| A. | $\frac{{y}^{2}}{2}-\frac{{x}^{2}}{3}$=1 | B. | y2-$\frac{{x}^{2}}{4}$=1 | C. | $\frac{{y}^{2}}{4}$-x2=1 | D. | $\frac{{y}^{2}}{3}-\frac{{x}^{2}}{2}$=1 |
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
| A. | -$\frac{197}{2}$ | B. | $\frac{197}{2}$ | C. | $\frac{183}{2}$ | D. | -$\frac{183}{2}$ |
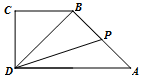 如图,在直角梯形ABCD中,AD∥BC,∠ADC=90°,AD=2,BC=CD=1,P是AB的中点,则$\overrightarrow{DP}•\overrightarrow{AB}$=-1.
如图,在直角梯形ABCD中,AD∥BC,∠ADC=90°,AD=2,BC=CD=1,P是AB的中点,则$\overrightarrow{DP}•\overrightarrow{AB}$=-1.