题目内容
如图,在四棱锥 中,四边形
中,四边形 是正方形,
是正方形, ,
, ,
, 分别为
分别为 的中点.
的中点.
(Ⅰ)求证:平面 平面
平面 ;
;
(Ⅱ)求二面角 的平面角的大小.
的平面角的大小.
(Ⅰ)祥见解析;(Ⅱ) .
.
解析试题分析:(Ⅰ)欲证平面EFG∥平面PCD,可根据面面平行的判定定理进行证明,即证明EG∥平面PCD,EF∥平面PCD;
(Ⅱ)取D为坐标原点DC为x轴,DA为z轴建立空间直角坐标,应用空间向量知识来求.也可取PC中点M,连接EM,DM,根据二面角的平面角的定义证明∠DEM就是二面角D-EF-B的平面角的补角,在△DEM中,即可求出二面角B-EF-D的平面角的大小.
试题解析:(Ⅰ)因为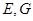 分别为
分别为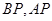 中点,所以
中点,所以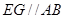 ,
,
又因为 是正方形,
是正方形,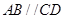 ,所以
,所以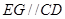 ,所以
,所以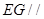 平面
平面 .
.
因为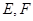 分别为
分别为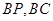 中点,所以
中点,所以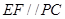 ,所以
,所以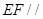 平面
平面 .
.
所以平面 平面
平面 .
.
(Ⅱ)法1.易知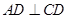 ,又
,又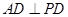 ,故
,故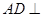 平面
平面
分别以 为
为 轴和
轴和 轴,建立空间直角坐标系(如图)
轴,建立空间直角坐标系(如图)
不妨设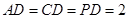 则
则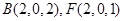 ,
,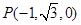
所以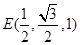
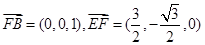
设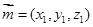 是平面
是平面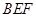 的法向量,则
的法向量,则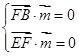 所以
所以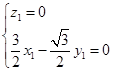 取
取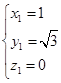 ,即
,即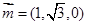
设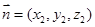 是平面
是平面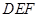 的法向量,则
的法向量,则 所以
所以 取
取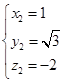
设二面角 的平面角的大小为
的平面角的大小为
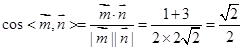
所以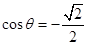 ,二面角
,二面角 的平面角的大小为
的平面角的大小为 .
.
法2.取 中点,联结
中点,联结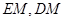 则
则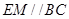 ,又
,又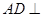 平面
平面 ,
,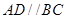 ,所以
,所以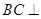 平面
平面 ,所以
,所以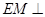 平面
平面
练习册系列答案
 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
 中,底面
中,底面 是正方形,
是正方形, ⊥平面
⊥平面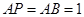 ,
,  ,
, 分别是
分别是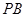 ,
,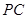 的中点.
的中点.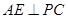
 到平面
到平面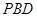 的距离.
的距离.
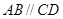 ,
,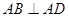 ,且
,且 .现以
.现以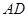 为一边向形外作正方形
为一边向形外作正方形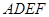 ,然后沿边
,然后沿边 为
为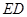 的中点,如图2.
的中点,如图2.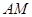 ∥平面
∥平面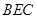 ;
;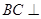 平面
平面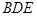 ;
; 到平面
到平面
 的底面为直角梯形,
的底面为直角梯形, ,
, 底面
底面 ,且
,且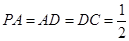 ,
,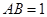 ,
, 是
是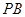 的中点.
的中点.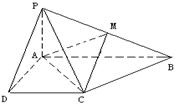
 面
面 ;
; 与
与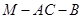 的正弦值.
的正弦值.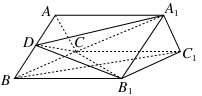
 的半径为2,圆
的半径为2,圆 是一小圆,
是一小圆, ,A、B是圆
,A、B是圆
 两点,若
两点,若 ,则A、B两点间的球面距离为 。
,则A、B两点间的球面距离为 。
 a,则它的5个面中,互相垂直的面有 对.
a,则它的5个面中,互相垂直的面有 对. 中,
中, ,
,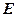 、
、 分别是
分别是 、
、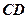 的中点,
的中点,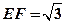 ,则异面直线
,则异面直线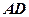 、
、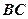 所成的角为 .
所成的角为 .