Question

过点B(0,-a)作双曲线x²-y²=a²右支的割线BCD,又过右焦点F作平行于BD的直线,交双曲线于G、H两点.

(1)求证:

(2)设M为弦CD的中点,S_△MBF= a²,求割线BD的倾斜角.

Answer 1

(1)证明:当a＞0时,设割线的倾斜角为α,则它的参数方程为(t为参数).                 ①?

则过焦点F且平行于BD的直线GH的参数方程为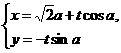(t为参数).                         ②?

将①代入双曲线方程,得t²cos2α+2atsinα-2a²=0.?

设方程的解为t₁、t₂,则有

BC·BD=t₁t₂=-,

同理,GF·FH=-FG·FH=-?

∴=2.?

同理,当a＜0时也得上述结果.

(2)解:当a＞0时,首先确定割线BD的倾斜角的范围,?

显然1＜tanα＜,?

于是,BM=

设F到BD的距离为d,则d=

∴tanα=或tanα=-(舍去).?

∴α=arctan.?

同理,当a＜0时,-＜tanα＜-1,可求得tanα=-,∴α=π-arctan.

∴BD的倾斜角为arctan(a＞0)或π-arctan(a＜0).