题目内容
14.x∈(0,+∞),证明:x+sinx≥-2ln(x+1).分析 由题意构造函数f(x)=x+sinx+2ln(x+1),由求导公式和法则求出f′(x),判断出f(x)在区间上的单调性、求出最小值,即可证明结论成立.
解答 证明:由题意构造函数f(x)=x+sinx+2ln(x+1),
则f′(x)=1+cosx+$\frac{2}{x+1}$>0,
所以函数f(x)在[0,+∞)上单调递增,
当x=0时,f(x)取到最小值f(0)=0,
所以当x∈[0,∞)时f(x)≥0恒成立,
则x+sinx≥-2ln(x+1)成立.
点评 本题考查证明不等式的方法:构造函数法,以及利用导数研究函数的单调性、最值问题,属于中档题.

练习册系列答案
相关题目
2.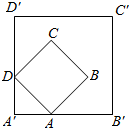 如图所示,边长为1的正方形ABCD的顶点A,D分别在边长为2的正方形A′B′C′D′的边A′B′和A′D′上移动,则$\overrightarrow{A'B}•\overrightarrow{A'C}$的最大值是( )
如图所示,边长为1的正方形ABCD的顶点A,D分别在边长为2的正方形A′B′C′D′的边A′B′和A′D′上移动,则$\overrightarrow{A'B}•\overrightarrow{A'C}$的最大值是( )
 如图所示,边长为1的正方形ABCD的顶点A,D分别在边长为2的正方形A′B′C′D′的边A′B′和A′D′上移动,则$\overrightarrow{A'B}•\overrightarrow{A'C}$的最大值是( )
如图所示,边长为1的正方形ABCD的顶点A,D分别在边长为2的正方形A′B′C′D′的边A′B′和A′D′上移动,则$\overrightarrow{A'B}•\overrightarrow{A'C}$的最大值是( )| A. | 2 | B. | 1+$\sqrt{2}$ | C. | π | D. | 4 |
9.函数y=1-2sinx的值域是( )
| A. | [-2,1] | B. | [-1,3] | C. | [0,1] | D. | [-2,3] |