题目内容
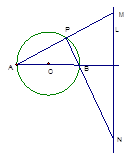
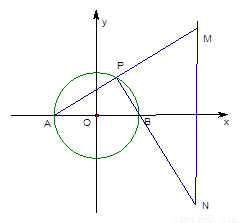
如图,已知圆O′过定点A(0,p)(p>0),圆心O′在抛物线x2=2py上运动,MN为圆在x轴上截得的弦,令|AM|=d1,|AN|=d2,∠MAN=θ.(1)当O′点运动时,|MN|是否有变化?证明你的结论.
(2)求![]() +
+![]() 的最大值,并求取得最大值时的θ值.
的最大值,并求取得最大值时的θ值.

解:(1)当O′点运动时,|MN|为一定值.
设O′(x0,y0),则x20=2py0(y0≥0),
取线段MN中点B,则有O′B⊥MN,所以有:
|M′N|=2|MB|=![]()
=![]()
=![]()
=![]() =2p.
=2p.
(2)在△AMN中运用余弦定理,得
|MN|2=|AM|2+|AN|2-2|AM||AN|cosθ![]() d21+d22-2d1d2cosθ=4p2, ①
d21+d22-2d1d2cosθ=4p2, ①
再由三角形的面积公式,在△AMN中可得:
![]() |AM||AN|sinθ=
|AM||AN|sinθ=![]() |MN||AO|
|MN||AO|![]() d1d2sinθ=2p2. ②
d1d2sinθ=2p2. ②
由①、②可得:
![]() +
+![]() =
=![]() =
=![]()
=2sinθ+2cosθ=2![]() sin(θ+
sin(θ+![]() )≤2
)≤2![]() ,
,
当sin(θ+![]() )=1时,
)=1时,![]() +
+![]() 取最大值2
取最大值2![]() ,
,
又0<θ<π,
所以取最大值时θ=![]() .
.

练习册系列答案
相关题目
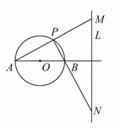
 如图,已知圆O的直径AB=4,定直线L到圆心的距离为4,且直线L垂直直线AB.点P是圆O上异于A、B的任意一点,直线PA、PB分别交L与M、N点.
如图,已知圆O的直径AB=4,定直线L到圆心的距离为4,且直线L垂直直线AB.点P是圆O上异于A、B的任意一点,直线PA、PB分别交L与M、N点.